This page explains the meaning of risk in investment and the relationship between risk and return, and also introduces the concept of expected value and variance.
The term investment risk is used, but there are many unclear points about its meaning.
Risk in investment is generally considered to be the degree of return uncertainty.
ref 1
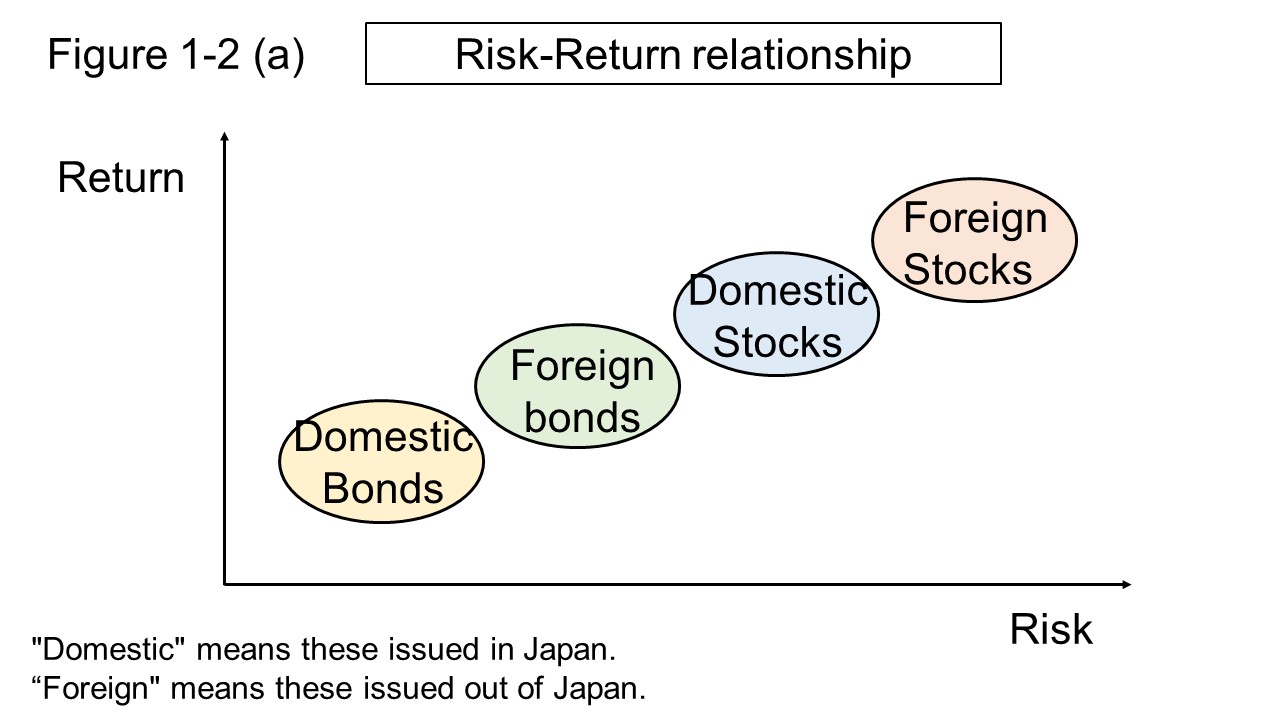
And, the terms high risk and high return and the diagram of relationship between risk and return as shown in Figure 1-2 (a) are often used to explain investment risk.
On the other hand, it is said that there are different types of risks.
ref 1
Various types of risk have been pointed out depending on the financial product, as follows.
|
|
However, in reality, the number of risks is not so many.
This is because all risks here are related to price fluctuations and are not independent.
The nouns crowned on all risks other than price fluctuation risk simply indicate the factor of price fluctuations.
The question is whether the risk of price fluctuation is the same as the risk which means the degree of return uncertainty.
If risk is the degree of return uncertainty, there should exist the center of return, but if risk is the price fluctuates, the existence of the center cannot be recognized.
Economic activity is not a natural phenomenon, and the center of asset prices cannot be determined.
Therefore, the risk, which is the degree of return uncertainty, is considered to be related from the past to the present, while the risk of price fluctuations is considered to be related from the present to the future.
When parents teach their children "it is dangerous to be hit by a car", they talk about danger for the future, but their recognition of danger has been formed in the past.
So, when it is said that there is a risk in investment, it can be interpleted plobably that the risk exist for the future but that the recognition of risk came from past events.
On the other hand, both the term "degree of uncertainty in returns" and "price fluctuations" have something in common that they do not state whether prices will rise or fall.
That is, unlike risks that are generally considered, the risks in investment do not mean only the bad things.
Therefore, the exact meaning of the risks in investment is interpreted as the price of any asset has fluctuated to some extent in the past, and if you invest, the asset price may continue to go up or down for the future.
Although it seems obvious, the risk cannot be recognized without knowing how much asset prices have changed in the past.
Considering the probabilities in terms of distribution, it is easy to imagine the relationship between risk and return shown in Figure 1-2 (a).
Figure 1-2 (b) show an image of past price movements for each asset class.
In the distribution of the rate of return of each asset, the expected value is the expected rate of return, and the variation in the rate of return is a risk.
In other words, the scale on the horizontal axis at the center of the distribution is the expected rate of return, and the width from the center of the distribution is the risk.
If the expected rate of return on stocks is 5-10%, that number probably represents the expected rate of return for the year, which corresponds to the center of the distribution of domestic and foreign stocks in Figure 1-2 (b).
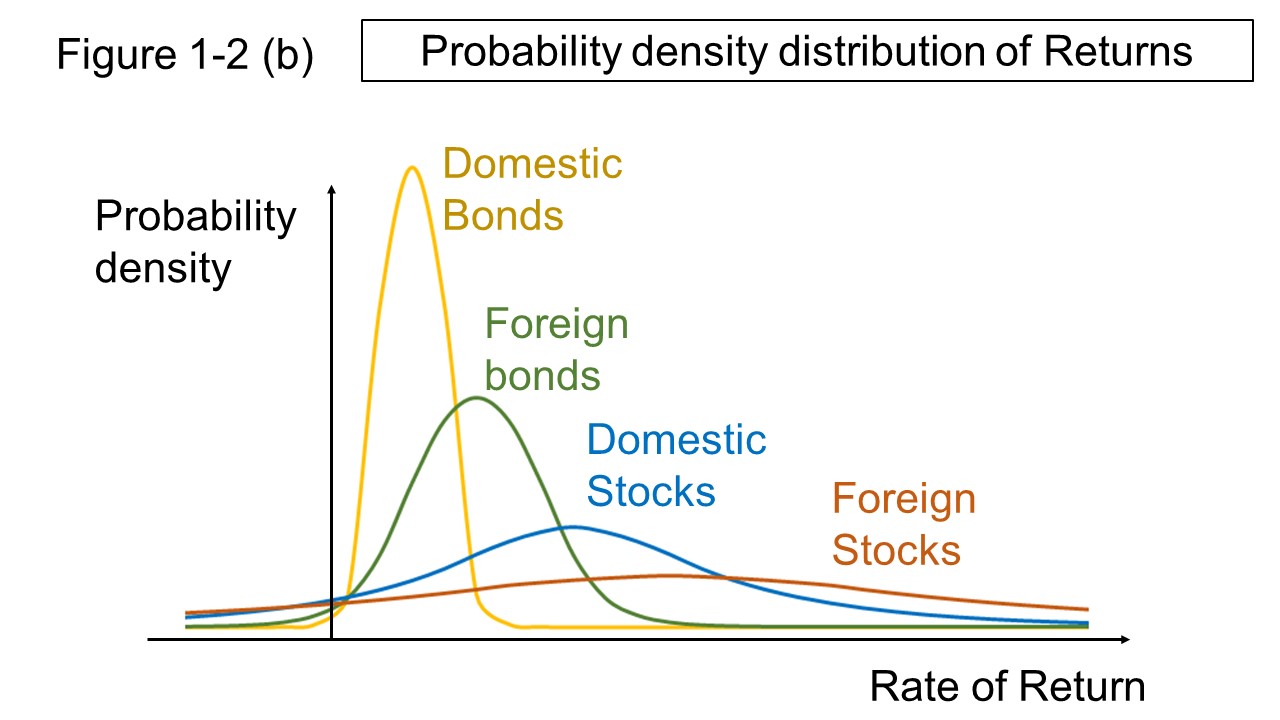
The first thing to understand about investing is the fact that the four assets shown in the figure have historically shown positive returns (at least since 1952).
This positive expectation is also the reason why investment is distinguished from gambling.
On the other hand, risk is often expressed by a statistical value called standard deviation (σ), which have been about 25% for stocks.
But, the range of ±1σ (±25%) from the expected value contains only about 68% of the data, and the spread (risk) of the distribution is larger than the value of the standard deviation.
This means that events outside the range of ±1σ occurred with a probability of about 1/3.
Now consider the game of rolling the strange die shown in Figure 1-2 (c).
The probability that the 1 to 6 rolls will appear at the top is known from the past statistics, and they are shown in the figure.
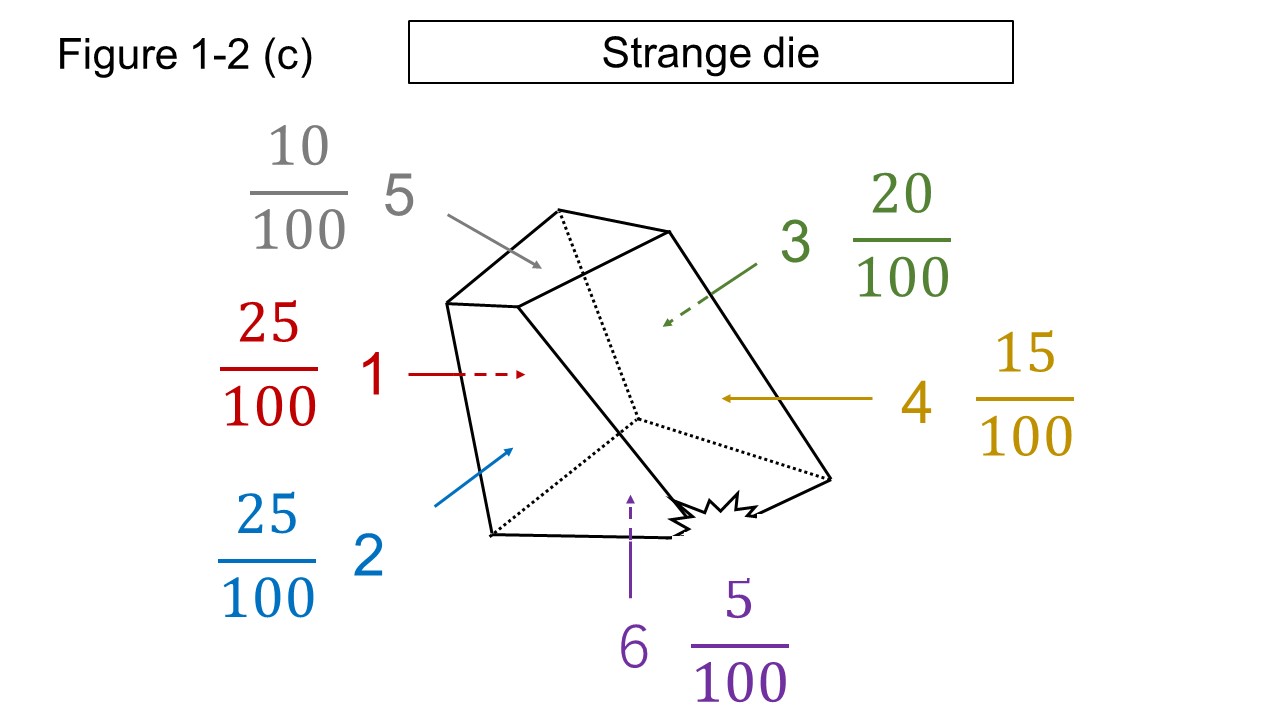
There are three games, and the bet is 100 yen for each game.
The die is rolled once a week and only one game can be chosen at that time.
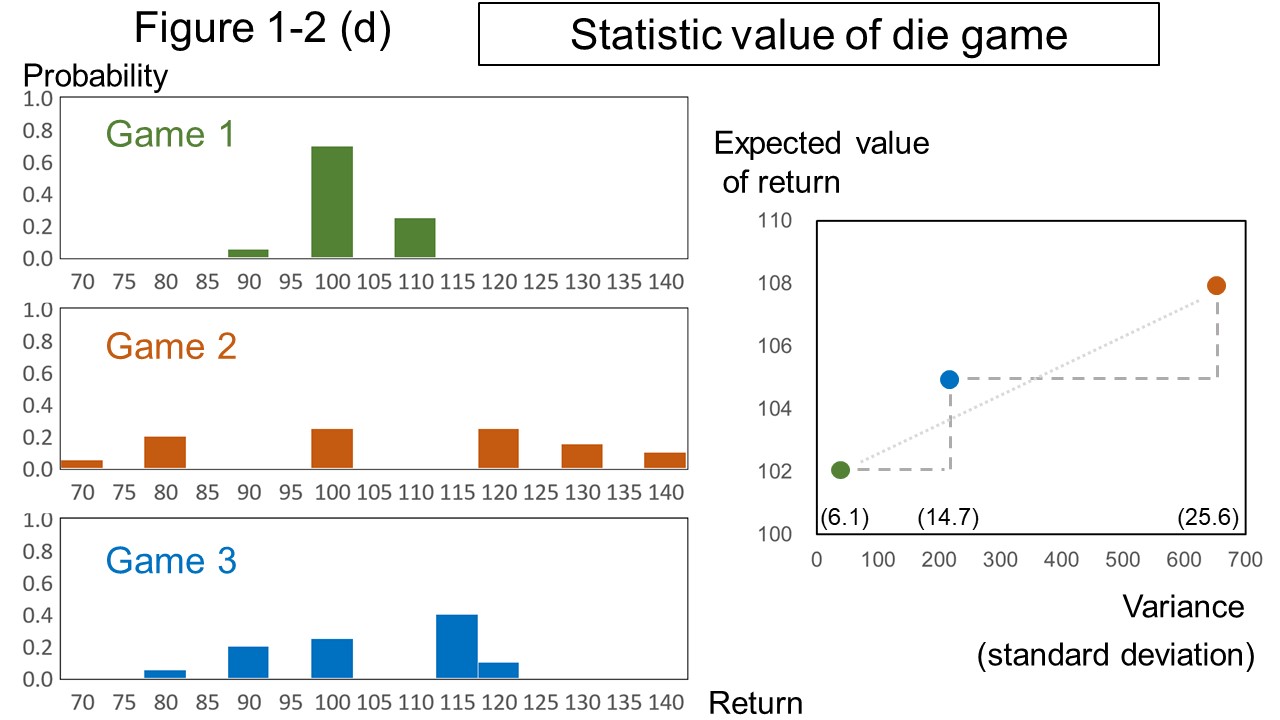
The returns from a roll of the die, expected value and variance for the dice roll on each game are summarized in the table below.
The rule of game 3 is that 50 yen are bet on both game 1 and game 2 at the same time, and the amount of return from each games is also half.
All games satisfy the condition of investment which show positive expected Value.
| A roll of the die | Probability | Retuen (yen) | ||
|---|---|---|---|---|
| Game 1 | Game 2 | Game 3 | ||
| 1 | 25/100 | 110 | 120 | 115 |
| 2 | 25/100 | 100 | 100 | 100 |
| 3 | 20/100 | 100 | 80 | 90 |
| 4 | 15/100 | 100 | 130 | 115 |
| 5 | 10/100 | 100 | 140 | 120 |
| 6 | 5/100 | 90 | 70 | 80 |
| Expected value | 102 | 108 | 105 | |
| Variance (Standard Deviation) | 37 (6.1) | 657 (25.6) | 217 (14.7) | |
Figure 1-2 (d) shows a graph of the values in this table.
In Game 1, you can't make a lot of money, but you won't lose a lot.
In Game 2, you can make a lot of money, but you may also lose a lot.
Despite only half betting on both Game 1 and Game 2, Game 3 seems that the positive return is large while it reduce probability of loss.
Which game is the best choice to bet on?
Game 2 shows the highest expected value.
If the law of large numbers is realized, return goes close to the expected value as the number of trial times increases.
Then, isn't it the most profitable and unlikely to lose the principal at least?
The question is how many trials can be repeated.
In the case of 1000 trial, the trial costs 100,000 yen, and the die will be rolled only 52 times a year under the condition of a weekly trial.
On the other hand, it is uncertin whether expectations will be realized for unsufficient number of trial times.
This is because the variance (standard deviation) indicates the range of possible results, and the average of the results will not converge to the expected value unless there is a reasonable number of trials for that range.
After all, which game to play seems to be related to the number of trials.
If you can increase the number of trial times, the game 2 showing a high expected value is advantageous.
However, it is necessary that the game is not over until the expectations are realized.
If you can't increase the number of trial times, the game 2 showing a low variance is acceptable.
The results around the expected value can appear with high possibility, so you can get steady profits without losing much.
And, in the game 3, since the variance is advantageous with respect to the expected value, high return can be expected moderately with a relatively small number of trial times.
Probability density distribution of returns shown in Figure 1-2 (b) and the histogram shown in Figure 1-2 (d) differ in terms of rate and amount, but their implications are almost the same.
However, there are some notable differences between dice games and investing.
The expected value and variance of the die game are the values obtained by accumulating one trial, but these of each asset are usually obtained based on the difference in asset price between the end of each year and the end of the next year.
Therefore, the possibility of larger price change from the end of the year to the beginning of the year is not included in the calculation of the expected rate of return and variance in the investment.
Also, in the die game, there is a refund for each trial, but in investment, bets will increase for each trial unless you sell it, and the invested money will not be returned for the time being.
As a result, positive or negative returns in investment are larger than expected, and in most cases the returns tend to be on accumulated cash rather than for one trial cash.
That said, there is no game with positive expected value other than investment.
Although past results do not assure the future, if the long-term data show positive expected value, it is well worth the investment.
It's not sure that the average of investment results will converge to the expected rate of return, but there is convincing evidence that the expected value of investment show positive.
It is the inequality “r> g” , which is showed in “Capital in the Twenty-First Century” by Thomas Piketty, and the steady economic growth in the past.ref 2
Also, what the expected rate of return and variance of each asset shows is the historical price changes of those assets, not changes of investor's asset.
In investment, you can improve the returns and risks of your assets, depending on how you bet.
In order to increase the return and reduce the risk, of own assets, it is necessary to know not only historical data but also schemes and techniques in investment.