On this page, investment and return is explained as basic knowledge that is the premise of investment.
In addition, this page introduce cash flow, which is an important concept of investment, and the way of thinking about money considering time.
Investing is the act of committing resources such as money, time, and effort in the expectation of a return.
In investment, of course, there is an object to be invested.
Investment targets include securities such as stocks, bonds, and mutual funds, and real assets such as real estate and gold.
The word "investment" is sometimes used like "self-investment" to enhance one's own value.
In the words of Warren Buffett, "By far the best investment you can make is in yourself."
ref1
Among them, the investments dealt with on this website relate to securities investments.
Hereafter, securities investment is simply referred to as investment.
One definition of investment is the act of putting money into an asset with the expectation of a positive return.ref2
Investing is not just about putting money in, it is also an activity that includes how to use the time until you get a return.
Investors have to decide not only whether to buy assets, but also whether to hold them or sell them.
An asset is any property that produces positive economic value, but the purchase of an asset does not always promise a positive return to the investor.
Therefore, there is a stricter definition.
Graham and Dodd state that "an investment operation is one which, upon thorough analysis, promises safety of principal and a satisfactory return".ref3
The former definition distinguishes investment from gambling, while the latter distinguishes investment from speculation.
Gambling is creating risks that didn't exist, and speculation is taking risks that are inherent in the situation.
“Gambling” represents the creation of risks not previously existing.
Whereas “speculation” applies to the taking of risks that are implicit in a situation and so must be taken by someone. ref3
The former definition of investment relates to whether or not to invest, while the latter definition relates to what to invest under what circumstances.
Investment based on the former definition is considered to bring long-term benefits even to investors who do not have the means to analyze investment targets.ref4
That's because past history has been showed positive long-term returns.
On the other hand, investors who follow the latter definition have to make analytical investment with "protection against loss under all normal or reasonably likely conditions or variations".ref3
On this website, the Investment basics section contains information about investing according to the former definition, and the Equity Investment section contains information about investing according to the latter definition.
Investment return is usually measured in terms of time as well as monetary value.
However, there is more than one return expression.
One expression of return is the rate of return, which indicates how much the value of an asset has increased or decreased.
On the premise that there is a period, the rate of return can be expressed by the following formula.
In this formula, \(V_{i}\) is the asset value at the beginning of the period, which is the basis of the rate of return.
\(V_{f}\) is the total value that the valuation at the end of the period or the proceeds from the sale of the asset plus any other income earned from the asset.
Rate of return is usually expressed as a percentage.
By defining a period, the rate of return becomes a measure that expresses the return over a certain period of time.
The rate of return over a period of one year is called annual return.
An annual return can represent the performance of an investment over a single year, but it is not suitable for representing the performance that has been repeated over many years.
The rate of return on investment over multiple years is often expressed as compound interest and the rate is called the compound annual growth rate (CAGR).
CAGR is expressed by the following formula.
CAGR is useful for representing investment performance when the investment principal remains unchanged.
On the other hand, it is difficult to use for investors who purchase assets with additional funds.
Therefore, Return on Investment (ROI) can be used as a simpler expression of return.
ROI is calculated by the following formula.
In this formula, \(C_{total}\) is the total cost of buying and selling assets.
\(V_{total}\) is the total valuethat the valuation at the end of the period or the proceeds from the sale of the asset plus any other income earned from the asset.
Simply put, ROI is net profit divided by total cost, over a period of time.
Using the formula below, ROI can be converted to an average annual growth rate called annualized ROI.
Annualized ROI is a simple and useful rate of return for investors who have acquired assets on a continuous basis to compare the performance of each asset and represent the overall performance of their investment.
Investing is the process of putting cash into an asset and getting a positive return over time.
There are two ways to get positive returns.
One is a way of obtaining a return by recovering more cash than the investment amount.
Another way is to obtain a return as a valuation gain on assets.
In investing, cash is recovered through periodic income such as interest/dividends or through redemptions/sales of securities.
The advantage of a cach recovered is that it can be used at will.
If you have cash, you can keep it or reinvest it.
The disadvantage is that the profits generated are taxable.
On the other hand, even if it is not necessarily collected as cash, the asset value will increase if valuation gains are generated.
The advantage of receiving valuation gains is that valuation gains are not taxed.
The disadvantage is that the use of assets is more restricted than cash.
In particular, assets with low liquidity can be difficult to convert to cash.
Whether to increase one's property as cash or as asset value depends on the intention of the investor. If the asset value goes up, the asset will increase whether you sell it or not. If your assets increase as cash, you can become rich, and if your assets increase as value, you can become a wealthy person.
Money flows are generated by buying, selling and holding assets. When you buy an asset, money flows out, and when you sell an asset, money flows in. Holding some assets provides regular income such as interest or dividends.
Such a flow of money is called cash flow. The flow of money coming in is called cash inflow and the flow of money going out is called cash outflow.
Figure 1-1 shows a conceptual diagram of cash flow in investment.
When focusing on the net amount of inflow and outflow, the difference between them is particularly called net cash flow, but on this website, it is called cash flow without distinction.
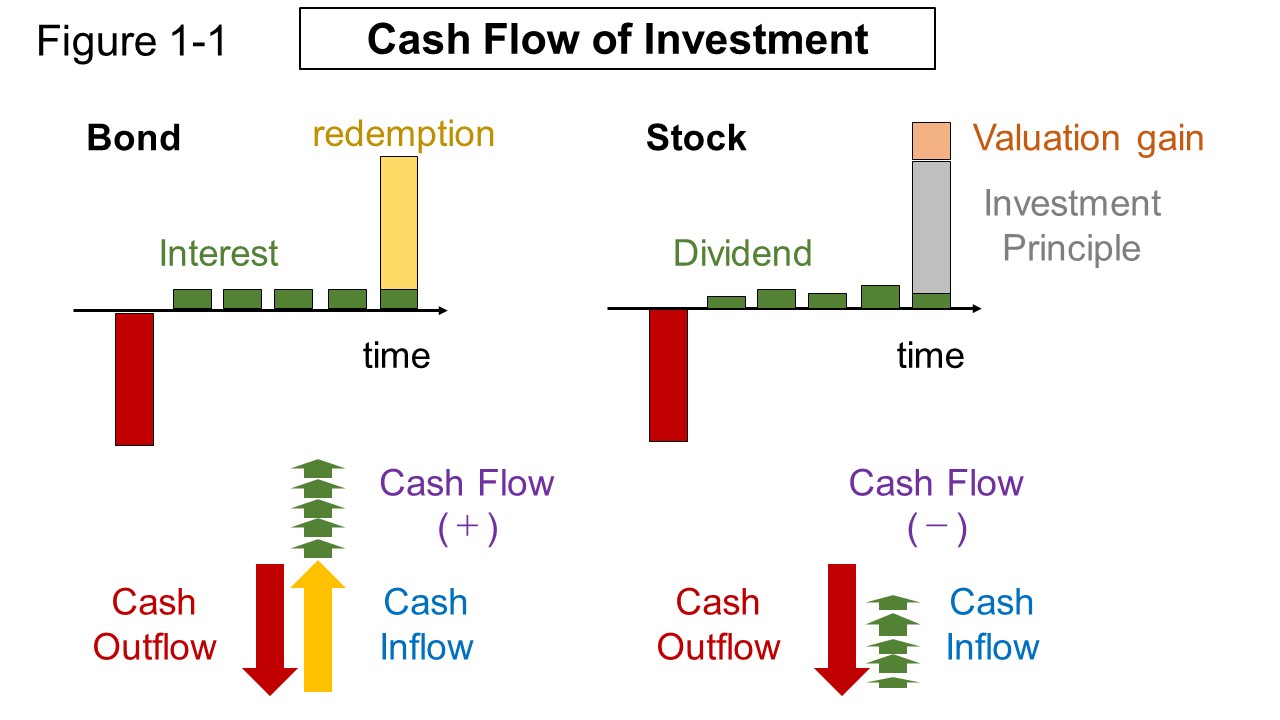
Bonds usually have the interest rate set and are returned at their face value at maturity.
Therefore, bonds issued by financially stable issuers until maturity are suitable for the purpose of securing the safety of principal and obtaining a stable cash inflow.
On the other hand, stocks have no maturity date and no predetermined price.
Investors have to decide how long to hold, how much to buy and how much to sell, depending on the situation.
Although stocks often show higher risk than bonds, the price uncertainty is also an advantage of stocks.
The price of a stock largely depends on the profits of the issuing company.
Therefore, the stocks of companies with stable profits are suitable for the purpose of obtaining cash inflows through dividends, since stock prices fluctuate relatively little.
On the other hand, stocks issued by companies with growing profits, or stocks that are undervalued by the market, are good candidates to eventually sell for a large cash inflow.
This concept of cash flow is important not only for investors' profits and losses, but also for considering the value of assets.
The creditworthiness of a security issuer, such as a country or a company, is judged by its cash flow.
The source of cash inflow is tax revenue for a country and operating revenue for a company.
And, whether it is a country or a company, their operations involve cash outflows.
Securities such as stocks and bonds, and the value of money, are affected by the creditworthiness of their issuers.
It is desirable that the company's cash flow is basically positive every year, and it is even more desirable that it will increase in the future.
A company with continuously negative cash flow will lose sources of investment for business growth, and in the worst case, it may go bankrupt when the cash needed to pay its debts runs out.
As it differs from the purpose of this page, cash flows related to corporate finance are explained on the page about cash flow statement.
We also detail the free cash flow a company generates on the page about company profitability.
On this page, please understand that cash flow is one of the most important concepts in investment.
To understand the basic idea of the value of an asset, consider the case where the interest rate on bank deposits is 5% per year as a simple example.
The basic idea of money is that the value of an asset is related to time.
If you deposit 1 million yen under the condition of an annual interest rate of 5%, 1.05 million yen will be collected one year later and you will make a profit.
Considering the time, the same can be rephrased as "the current 1 million yen has the same value as 1.05 million yen one year later.
When you consider that "1 million yen becomes 1.05 million yen after one year under the condition of an annual interest rate of 5%", the future value can be calculated by the following formula.
On the other hand, when you consider that "the current 1 million yen has the same value as 1.05 million yen one year later under the condition of an annual interest rate of 5%",
the current value can be calculated by the following formula.
The left-hand side of this equation represents the present value, while on the right-hand side, the numerator is the future value and the denominator is the annual interest rate.
At first glance, it looks like the formula has just been transformed,but the advantage of this idea is that you can decide if you should invest under certain conditions.
For example, when the deposit interest rate of a bank is 5% per year, what is the discounted present value of zero coupon bonds that will surely return at 10 million yen one year later?
Assuming that the amount to be invested now is \(x\) million yen, it will be \(x\) × 1.05 million yen one year later just by depositing in a bank.
So unless the price is lower than the solution of the following formula (9.52 million yen), it turns out that it is better to deposit in the bank than to buy the bond.
For example, when the deposit interest rate of a bank is 5% per year, what is the discounted present value of zero coupon bonds that will surely return at 10 million yen two year later
In addition, when the deposit interest rate of a bank is 5% per year, the discounted present value of zero coupon bonds that will surely return at 10 million yen after two years is 9.07 million yen from the following formula.
In this way, the future value is discounted at a certain discount rate, and the value expressed as the present value is called the discounted present value.
An analytical model that sets a certain discount rate and values the discounted present value of an asset from future cash flows is called a discount cash flow model.
An analytical method for valuing assets based on that model is known as the discounted cash flow (DCF) analysis.
Since the detailed explanation of the DCF method is beyond the scope of this page, only the outline of the DCF method will be explained here using FIRE (Financial Independence Retire Early) as an example.
The goal of FIRE is to build a certain amount of assets and maintain a livelihood from the profits.
So, let's consider a case that you build an asset of 100 million yen at the age of 40 and will make a living by 4% annual yield (4 million yen) to the age of 60 with maintaining the assets.
If the inflation rate is 2% or 5%, how much is the present value of the 4 million yen and of assets that you plan to receive at the age of 60?
The following table summarizes the discounted present value of the amount that you can receive by the age of 60.
If the inflation rate is 0%, the future monetary value will be the same as it is now, but if the inflation rate is positive, the monetary value will be discounted accordingly.
If the inflation rate is 2%, what you receive at the age of 60 are income with a present value of 2.69 million yen (face value of 4 million yen) and assets with a present value of 67.3 million yen (face value of 100 million yen).
At this level, FIRE can be successful, and you may be able to live confortably by monetizing the assets.
On the other hand, if the inflation rate is 5%, the present value of income at the age of 60 is 1.51 million yen and the present value of assets is 37.69 million yen, so it may be difficult to live after that.
| Inflation rate | Discounted Present Value (yen) | |||||
| 1st year | 2nd year | 3rd year | … | 20th year | assets | |
| 0% | 4.00 million | 4.00 million | 4.00 million | … | 4.00 million | 100 million |
| 2% | 3.92 million | 3.84 million | 3.77 million | … | 2.69 million | 67.30 million |
| 5% | 3.88 million | 3.63 million | 3.46 million | … | 1.51 million | 37.69 million |
In this way, the DCF method can treat the value of assets in future as the present value.
The details of the DCF method are described on another page.
The linked page describes an example of calculating enterprise value (EV) using the DCF method.