本ページでは、投資の前提となる基礎知識として、投資とリターンについて説明する。
加えて、投資の重要な概念であるキャッシュ・フローと、時間を考慮したお金の考え方について紹介する。
投資とは、リターンを期待して、お金、時間、労力のような資源を投じる行為である。
投資では、当然ながら、投資される対象が存在する。
投資対象には、株式・債券・投資信託のような証券や、不動産・金のような実物資産など、様々なものがある。
投資という言葉は自らの価値を上げるための「自己投資」のように使われることもある。
Warren Buffettは、"By far the best investment you can make is in yourself."と述べている。
ref1
その中でも、本ウェブサイトで扱う投資は、証券投資に関するものである。
以降、証券投資を単に投資という。
投資の1つの定義は、プラスのリターンを期待して資産にお金を投じる行為のことである。ref2
投資は、単にお金を投じることだけでなく、リターンを得るまでの過ごし方をも含む活動である。
投資家は、資産を買うことだけでなく、維持するか売却するかを判断する必要がある。
資産とはプラスの経済的価値を生み出す財産のことであるが、資産を購入すれば投資家にプラスのリターンが約束される訳ではない。
そこで、より厳しい定義もある。
GrahamとDoddは、「投資とは、徹底的な分析に基づき、元本の安全性と満足のいくリターンを与える営みである」とする(Graham, Dodd 1934 引用者訳)。ref3
前者の定義では投資はギャンブルと区別され、後者の定義では投資は投機と区別される。
「"ギャンブル"とは存在しなかったリスクを創り出すこと」である。
一方で、「"投機"とは状況に内在し、誰かが取るべきリスクを取ること」である(Graham, Dodd 1934 引用者訳)。ref3
投資に関する前者の定義は投資をするか否かに関係し、後者の定義はどのような状況で何に投資するかに関係している。
前者の定義に基づく投資は、投資対象を分析する手段を持ち合わせていない投資家にとっても長期的にメリットをもたらすと考えられている。ref4
過去の歴史が長期的にプラスのリターンを示してきたからである。
一方で、後者の定義に従う投資家は、「普通にあるいは合理的に起こりそうな状況や変化の下で損失に対する保護を備えた」分析的な投資をする必要がある。(Graham, Dodd 1934 引用者訳)ref3
本ウェブサイトでは、投資の基本のセクションに前者の定義に基づく投資に関する内容が、株式投資のセクションに後者の定義に基づく投資に関する内容が掲載されている。
投資のリターンは、通常、金銭的価値だけでなく時間も考慮された上で測られる。
しかし、リターンの表現は1つではない。
リターンの1つの表現は、当初の資産価値がどの程度増減したかを表す収益率である。
収益率は、期間があることを前提として、以下の式で表すことができる。
この式において、 \(V_{i}\) は収益率の基礎となる期初の資産価値である。
\(V_{f}\) は期末の評価価値あるいは売却により得られた収入に、その資産から得られた他の収入も加えた全ての価値である。
収益率は、通常パーセンテージで表される。
期間を定めることで、収益率は一定期間のリターンを表す指標となる。
期間が1年間の収益率はannual returnと呼ばれる。
annual returnはある1年間のリターンを表すことはできるが、何年も繰り返された投資のパフォーマンスを表すことには適していない。
複数年にわたる投資の収益率は、複利で表されることが多く、その利率はCompound annual growth rate (CAGR)と呼ばれる。
CAGRは以下の式で表される。
CAGRは、投資元本が変化しない場合の投資パフォーマンスを表す場合に有用である。
一方で、追加的な資金で資産を購入する投資家にとっては使いにくい面がある。
そこで、より簡便なリターンの表現として、投資収益率(ROI : Return on Investment)を用いることもできる。
ROIは以下の式で計算される。
この式において、 \(C_{total}\) は資産の購入および売却に要した全ての費用である。
\(V_{total}\) は現在の資産の価値、あるいは売却により得られた収入に、その資産を所持することによって得られた収入を加えた全ての価値である。
平たく言えば、ROIはある期間の純利益を総費用で割ったものである。
以下の式を用いると、ROIはannualized ROIと呼ばれる年平均の成長率に換算することができる。
Annualized ROIは継続して資産を取得した投資家にとって、各資産のパフォーマンスを比較したり、投資全体でのパフォーマンスを表すのに使いやすい収益率である。
投資とは資産へキャッシュを投入し、時間をかけて、プラスのリターンを得る一連のプロセスである。
プラスのリターンを得る方法は、2通りある。
1つは投資額よりも多くのキャッシュを回収することでリターンを得る方法である。
もう1つは、資産の評価益としてリターンを得る方法である。
投資においては、キャッシュは、利息・配当のような定期的な収入、あるいは証券の償還・売却によって回収される。
回収されたキャッシュのメリットは、そのキャッシュを自由に使えることである。
キャッシュがあれば、手元に置いておくことも、再投資することもできる。
デメリットは、得られた利益に対して課税されることである。
一方で、必ずしもキャッシュとして回収しなくても、評価益が発生すれば資産価値は増加する。
評価益を享受するメリットは、評価益に対しては課税されないことである。
デメリットは、資産の用途はキャッシュよりも制限されていることである。
特に、流動性の低い資産は、現金化することが難しい場合がある。
自らの財産を、キャッシュとして増やすか、資産価値として増やすかは、投資家の志向による。
資産価値が上がれば、売却するかしないかにかかわらず、資産は増加する。
資産がキャッシュとして増えれば金持ちになれるし、価値として増えれば資産家になれる。
資産の売買や保持によって、お金の流れが発生する。
資産を買うとキャッシュが流出し、資産を売却するとキャッシュが流入する。
資産によっては保持することで利息や配当のような定期的な収入が得られる。
このようなお金の流れのことをキャッシュ・フローという。
入ってくるお金の流れをキャッシュ・インフロー、出ていくお金の流れをキャッシュ・アウトフローという。
投資でのキャッシュ・フローの概念図を図1-1に示した。
インフローとアウトフローの正味額に注目するとき、それらの差額を特にネット・キャッシュ・フローと呼ぶが、本ウェブサイトでは特に区別せずにキャッシュ・フローと呼ぶ。
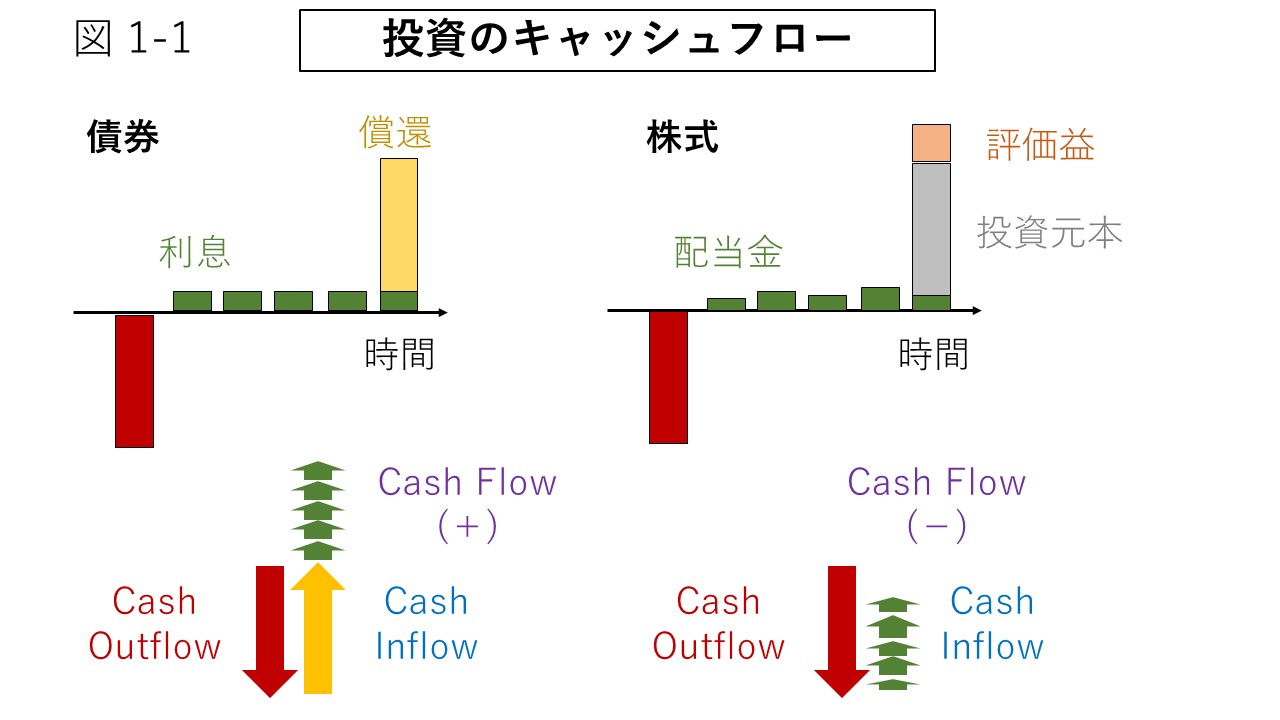
債券は通常、金利が定められており、償還期限を迎えると額面金額で戻ってくる。
そのため、償還期限まで財務が安定していることが期待される発行体による債券は、元本の安全性を確保しながら安定したキャッシュ・インフローを得る目的に適している。
一方で、株式には償還期限がなく、事前に定められた価格もない。
いつまで持つか、あるいは、いくらなら買い、いくらなら売るかといったことは、投資家が状況に応じて判断する必要がある。
株式はしばしば債券よりも高いリスクを示すものの、その価格の不確実性は株式のメリットでもある。
株式の価格は、その発行企業の利益に依存する面が大きい。
そのため、利益が安定した企業の株式は比較的株価の変動が小さく、配当によるキャッシュ・インフローを得る目的に適している。
一方で、利益が成長している企業の株式や市場が評価を間違えた株式は、いつの日か売却することにより、大きなキャッシュ・インフローを得る目的に適している。
このキャッシュ・フローの概念は、投資家の損得だけではなく、資産の価値を考える上でも重要である。
国や企業のような証券の発行体の信用力は、そのキャッシュ・フローに基づいて判断される。
国であれば税収、企業であれば営業収益がキャッシュ・インフローの源泉である。
そして、国であれ企業であれ、その運営にキャッシュ・アウトフローを伴う。
株式や債券のような証券、およびお金の価値は、その発行体の信用に影響を受ける。
企業のキャッシュ・フローは、基本的に毎年プラスであることが望ましく、将来増加することがさらに望ましい。
キャッシュ・フローが継続してマイナスの企業は、事業の成長のために投資する源泉を失い、最悪の場合、債務の支払いに必要なキャッシュが枯渇して倒産することもあり得る。
本ページの趣旨とは異なるため、企業の財務に関連するキャッシュ・フローについては、
キャッシュフロー計算書のページ
で説明している。
また、企業が生み出すフリー・キャッシュ・フローについても、
収益力の指標のページ
で詳しく説明している。
本ページでは、キャッシュ・フローは、投資におけるもっとも重要な概念の1つであることを理解されたい。
資産の価値に対する基本的な考え方を理解するため、簡単な例として銀行預金の金利が年5%である場合について考える。
お金に対する基本的な考え方は、資産の価値は時間と関係があるということである。
例えば、年利5%の条件で100万円を預金すると、1年後には105万円回収されて儲かる。
時間を考慮すると、同じことが「現在の100万円には1年後の105万円と同じ価値がある」と言い換えられる。
「年利5%の条件では、100万円が1年後に105万円になる。」と考えるとき、将来の価値は以下の式で求まる。
一方で、「年利5%の条件では、現在の100万円は1年後の105万円と同じ価値がある」と考えるとき、現在の価値は以下の式で求まる。
この式の左辺が現在の価値であり、右辺は分子が将来の価値、分母が年利である。
一見数式を変換しただけだが、この考え方のメリットは、どのような条件であれば投資すべきかを判断できる点にある。
例えば、銀行の預金金利が年5%のとき、1年後に確実に1,000万円で返ってくるゼロ・クーポン債の割引現在価値はいくらだろうか?
今投資すべき金額を \(x\) 万円とすると、銀行に預金するだけで1年後に \(x\) × 1.05 万円になる訳であるから、 以下の式の解(952万円)よりも低い価格でなければ、その債券を買うより銀行に預金した方がよいことが分かる。
なお、銀行の預金金利が年5%のとき、2年後に確実に1,000万円で返ってくるゼロ・クーポン債の割引現在価値は、以下の式から907万円となる。
このように、将来得られる価値をある割引率で割り戻し、現在の価値として表したものを割引現在価値という。
ある割引率を設定し、資産が将来生み出すキャッシュ・フローからその資産の割引現在価値を見積もる分析のモデルを割引キャッシュ・フローモデルという。
そのモデルに基づいて資産を評価する分析手法は、割引キャッシュ・フロー法(DCF法 : Discount Cash Flow法)として知られている。
DCF法の詳細な内容については本ページの趣旨から外れるため、ここではFIRE(Financial Independence Retire Early)を例にとってDCF法の概要を説明する。
FIREの目指すところは、一定の資産を築き、その収益で生計を維持するというものである。
そこで、仮に40歳で1億円の資産を築き、その元本を維持したまま4%の年間益回り(400万円)で60歳まで生活する場合について考える。
インフレ率が2%あるいは5%であった場合、60歳になったときに受け取る予定の400万円と元本は、現在どの程度の価値があるだろうか?
下の表に60歳までに受け取る金額の割引現在価値をまとめた。
インフレ率が0%の場合、将来の貨幣価値は現在と同じであるが、インフレ率が正であった場合、その分の貨幣価値が割り引かれていく。
インフレ率が2%の場合に60歳で受け取る金額は、現在価値で269万円の額面400万円と、現在価値で6,730万円の資産1億円である。
この程度であれば、FIREは成功し、その後も資産を取り崩せば生活ができるかもしれない。
一方で、インフレ率が5%の場合の受取金額は、現在価値で151万円の額面400万円と、現在価値で3,769万円の資産1億円となり、余裕のある生活は難しいかもしれない。
| インフレ率 | 割引現在価値(円) | |||||
| 1年目 | 2年目 | 3年目 | … | 20年目 | 資産 | |
| 0% | 400万円 | 400万円 | 400万円 | … | 400万円 | 1億円 |
| 2% | 392万円 | 384万円 | 377万円 | … | 269万円 | 6730万円 |
| 5% | 388万円 | 363万円 | 346万円 | … | 151万円 | 3769万円 |
このように、DCF法は将来の資産価値を現在の価値として扱うことができる。
なお、DCF法の詳細な内容は、別のページに記載した。
リンク先のページでは、DCF法を用いた事業価値(EV)の計算例を記載している。