本ページでは、長期投資のシミュレーションと、資産運用の具体的な手法について紹介する。
ある期待収益率を設定すると、自分の想定する投資期間に応じてその経過をシミュレーションすることができる。
それほど難しい式は必要なく、以下の式でゴールの金額を設定し、そのゴールへの道のりを変えてみるだけである。
ゴールの金額 = 投資資金 × (1 + ERR)n
ERR : 期待収益率(年)
n : 想定する投資期間(年)
現実にはゴールは未確定であり、「当たるも八卦、当たらぬも八卦」である。
しかし、ゴールへの道のりは複雑であるため、妥当な期待収益率であれば、
ゴール時点が正確でなくてもゴールの金額には到達する可能性はある。
ここでは、年4.3%の期待収益率での資産運用について考える。
適当ではあるが、標準偏差を20%とし、以下の表1のような収益率で30年を経過したとする。
標準偏差が20%であれば、±20%以内(±1σ 範囲内)の価格変動が起きる確率が68%であり、それよりも変動が大きい確率が32%である。
| 年数 | 1年目 | 2年目 | 3年目 | 4年目 | 5年目 | 6年目 | 7年目 | 8年目 | 9年目 | 10年目 |
| 収益率 | −10% | −35% | 0% | +10% | −10% | +35% | +15% | +35% | +5% | −10% |
| 年数 | 11年目 | 12年目 | 13年目 | 14年目 | 15年目 | 16年目 | 17年目 | 18年目 | 19年目 | 20年目 |
| 収益率 | −30% | +5% | +15% | +35% | −5% | +10% | +25% | +15% | +5% | +20% |
| 年数 | 21年目 | 22年目 | 23年目 | 24年目 | 25年目 | 26年目 | 27年目 | 28年目 | 29年目 | 30年目 |
| 収益率 | +10% | −25% | +20% | −5% | −5% | 0% | +15% | +20% | +5% | +10% |
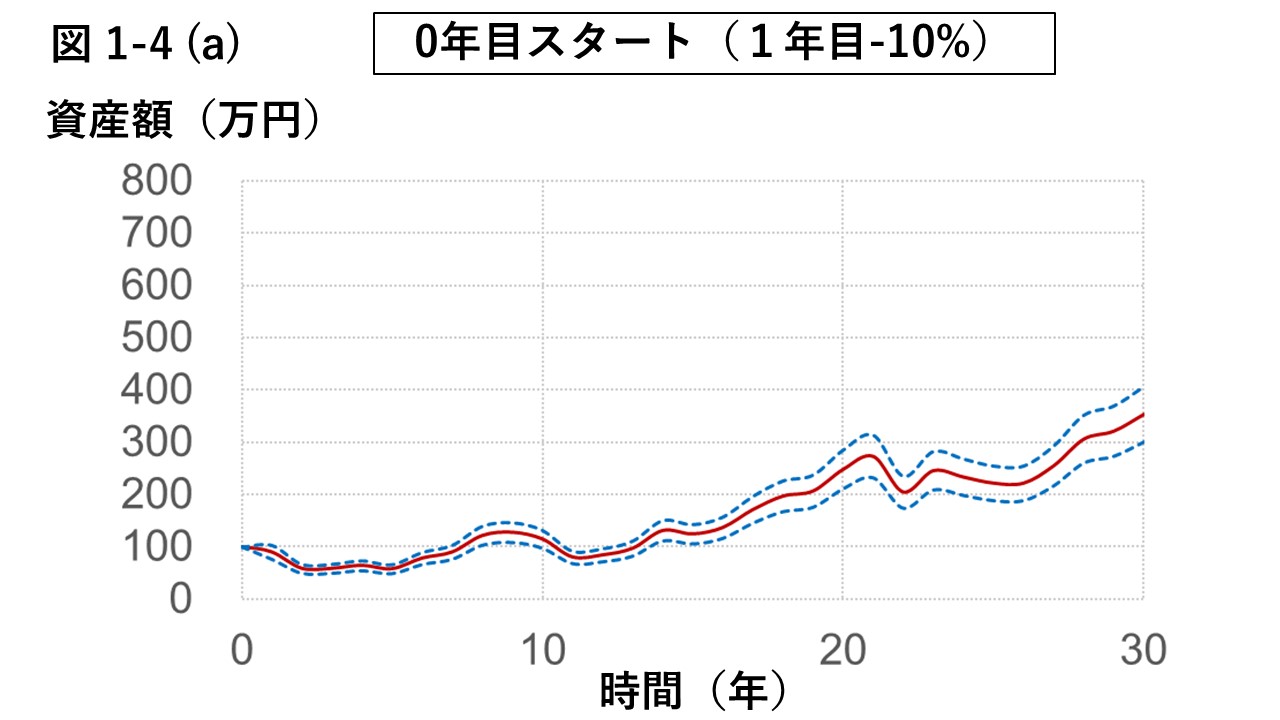
表1の損益をグラフ化したものが、図1-4 (a) ”0年目スタート”である。
青の点線は、赤線から±15%の範囲を示す、上記の標準偏差とは別の、資産価格の年間の変化を表しものである。
あえて青線の点線を加えた理由は、年間の変動により、
想定したタイミングでなくとも目的の資産額に到達する可能性があることを示すためである。
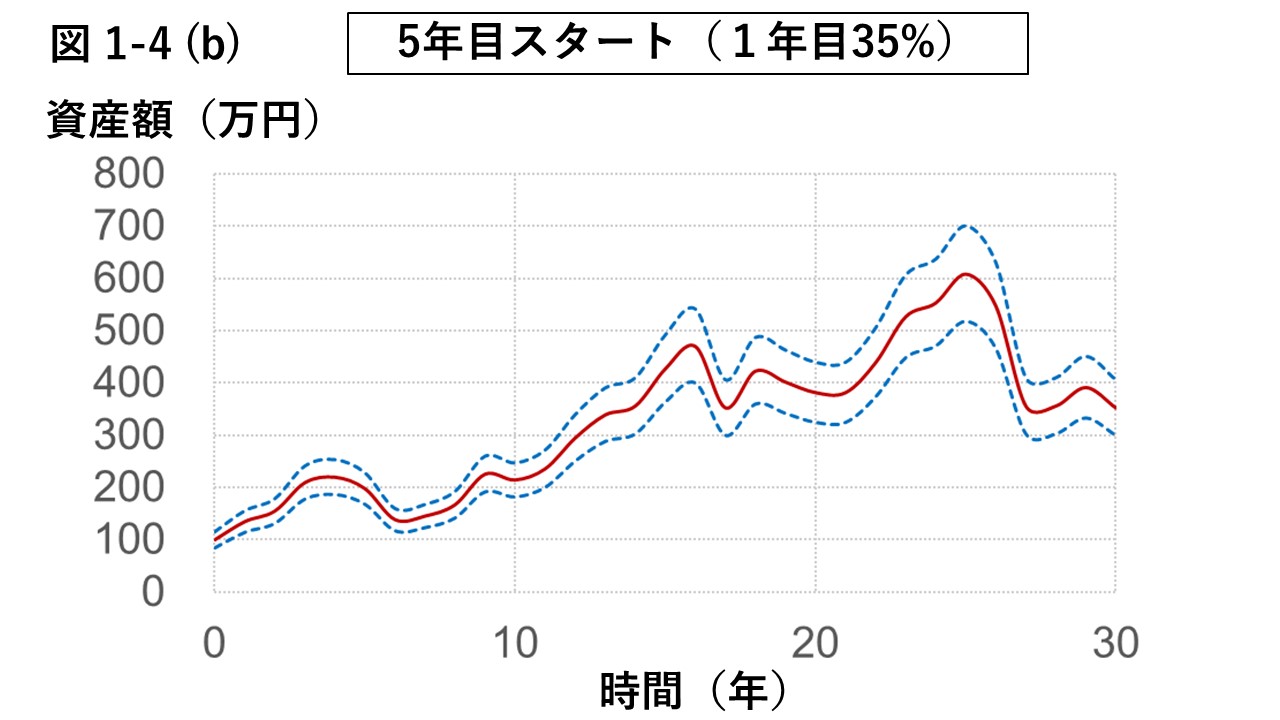
そして、5年目から投資をスタートし、5年目までの収益率を後に追加した場合の損益をグラフ化したものが、 図1-4 (b) "5年目スタート"である。
\(n\) 年目の収益率を\(R_{n}\)としたとき、
"0年目スタート"と"5年目スタート"の期待収益率はいずれも式(1)で表される。
そのため、どちらの場合も最終的なゴールは同じである。
しかし、ゴールに至るまでの道筋はだいぶ異なる。
”0年目スタート”は、序盤の5年間に大きな損失を伴う、不運なスタートと言える。
13年目まで鳴かず飛ばずで、その後ようやくリターンがプラスになり始める。
最終的には、上昇基調で約300万円に到達する。
一方で、”5年目スタート”は、序盤の5年間に大きな利益を伴う、幸運なスタートと言える。
投資金額を割り込むことなく、資産額は一時的に600万円にもなっている。
しかし、その後は急降下し、最終的には約300万円となる。
このシミュレーションは、以下のことを示唆している。
- 期待収益率が定まっているのであれば、道筋はどうであれ、やがて同じゴールに行き着く。
- スタートのタイミングは、その後の資産価格の推移に影響を与える。
- スタートのタイミングと同様に、エグジットのタイミングも重要である。
しかし、投資タイミングを読める者は5年目から投資をすることも可能だが、5年も先のことはなかなか分かるものではない。
資産の分散以外に、複数のタイミングで資産を購入することも投資成果に影響を与える。
ref 1
とはいえ、複数のタイミングで資産購入する方法はいくらでも存在する。
ここでは定期的な投資に限り、一定金額での資産購入と一定数量での資産購入について考える。
前者はドル · コスト平均法と呼ばれ、後者と比較して低い平均取得単価で資産を購入できることが知られている。
2つの方法を比較するにあたり、後者にも名前がないと不便なので、ここではドル · 数量累積法と呼ぶことにする。
- ドル · コスト平均法
- 定期的に、一定金額で資産を購入する方法
- ドル · 数量累積法
- 定期的に、一定数量の資産を購入する方法
以下、株価が1株100円から変化する際に、 ドル · コスト平均法で毎月100円分の株を購入する場合と、ドル · 数量累積法で毎月1株を購入する場合について考える。
図1-4 (c)は、年初と年末が1株100円で、その間の株価が70円から130円の間で推移した"横ばいチャート"である。
この場合の平均取得単価は、ドルコスト平均法では1株=92.4円、ドル · 数量累積法では1株=100.0円となり、
ドル · コスト平均法の方が低い平均取得単価を示す。
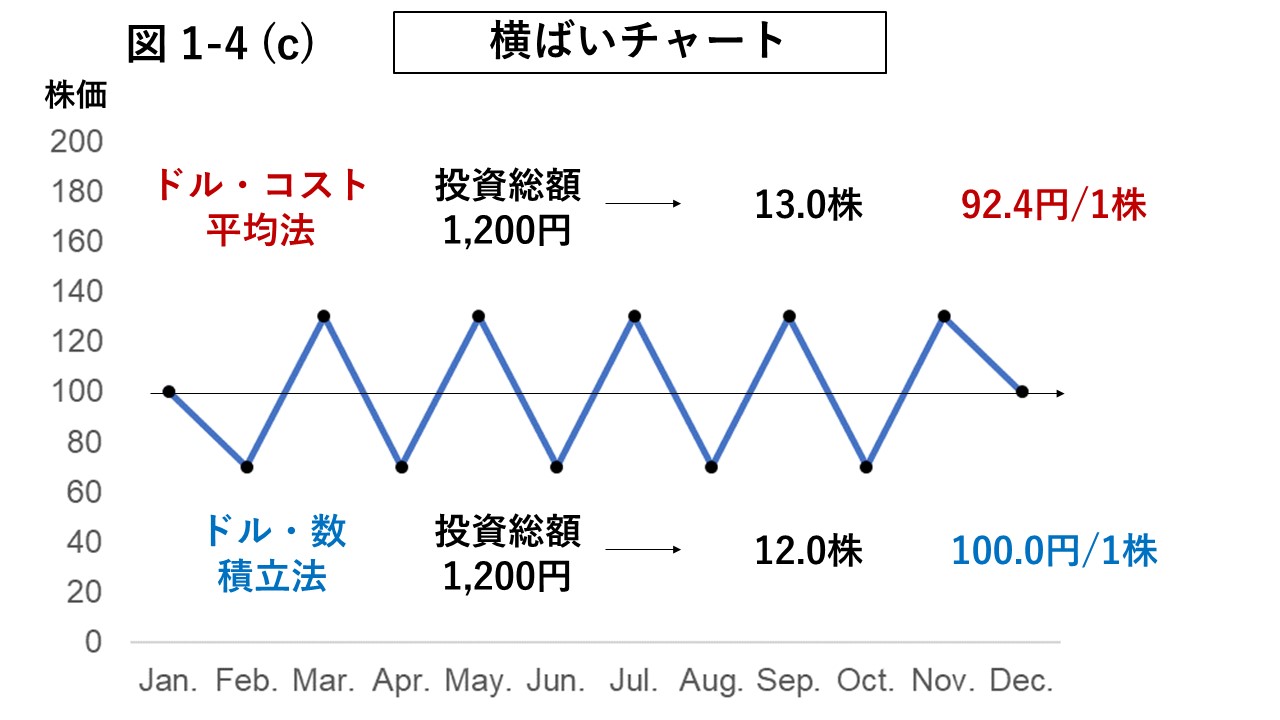
しかし、平均取得単価が下がることは、必ずしも儲かったり損失額が減ったりすることを意味しない。
下に示した図1-4 (d)と図1-4 (e)は、それぞれ株価が上昇と下落の傾向を示す、互いに上下を反転させたチャートである。
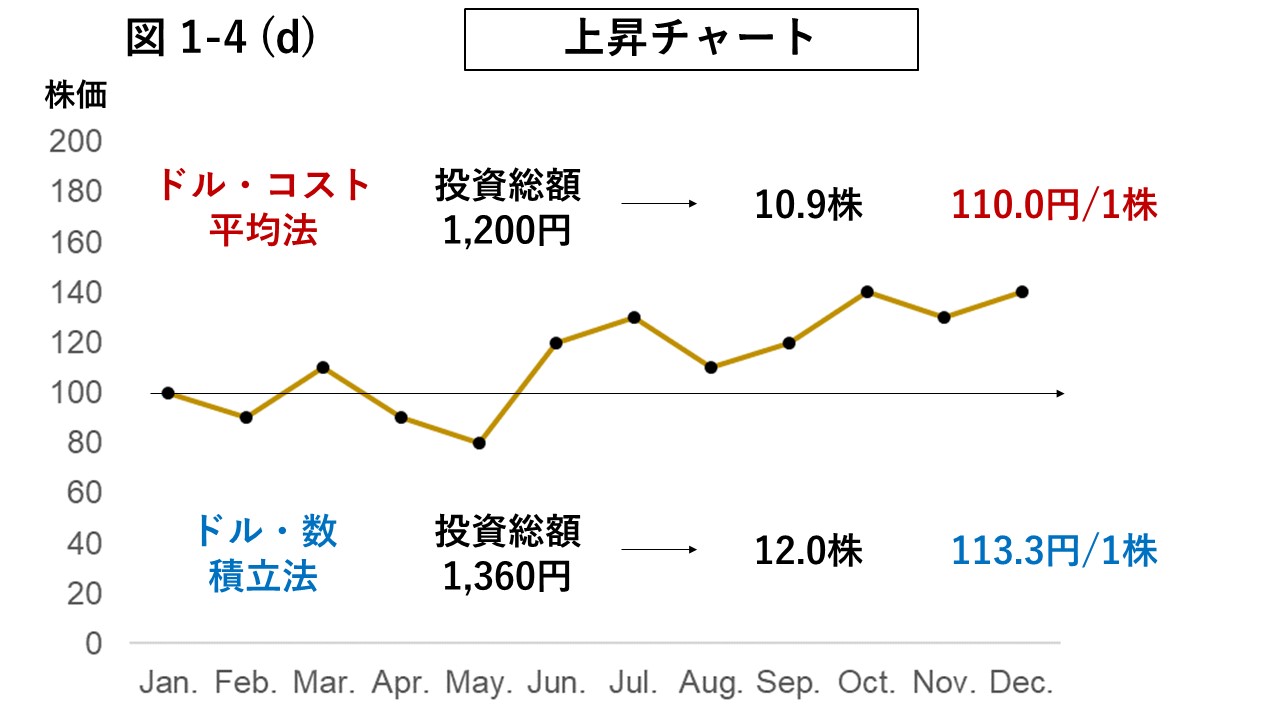
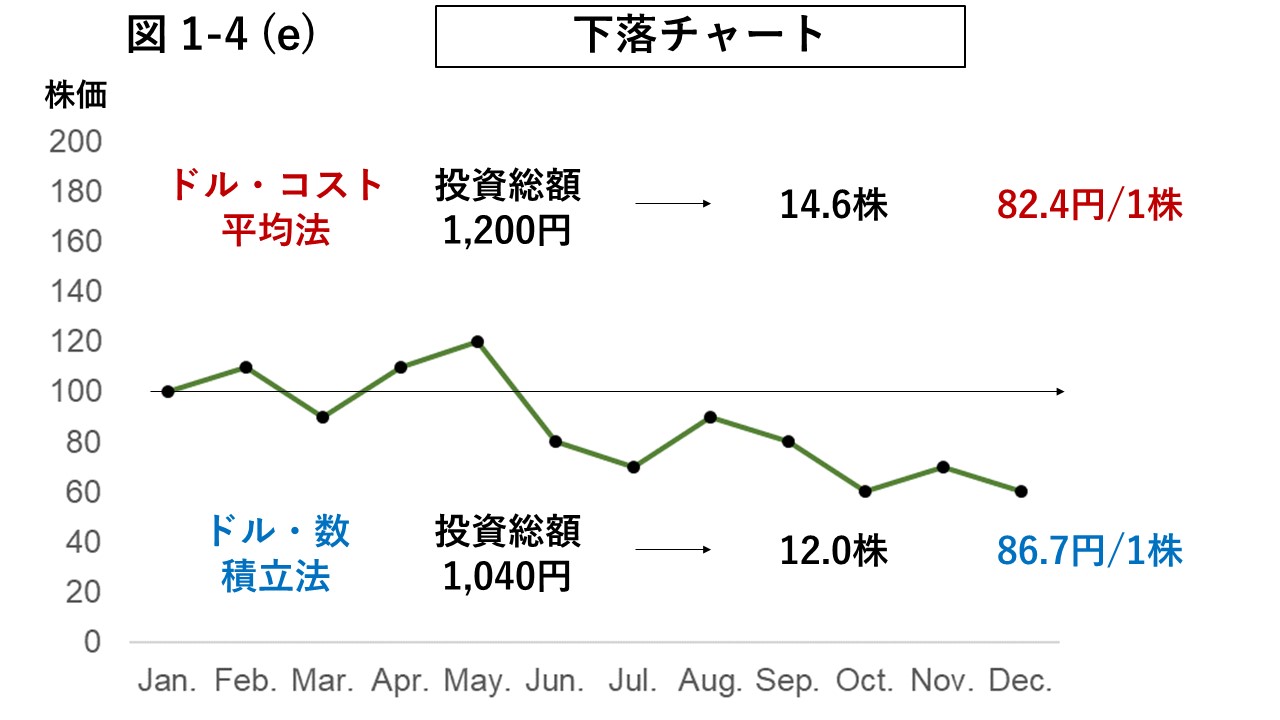
これらの2つのチャートでドル · コスト平均法とドル · 数量累積法を比較したものが表2である。
平均取得単価は株価の方向にかかわらずドル · コスト平均法の方が低い。
しかし、損失額は株安時のドル · コスト平均法が最も大きいことが分かる。
| チャート/方法 | 保有株数 | 平均取得単価 | 投資総額 | 損益 | 損益率 | |
| 株高 | ドル · コスト平均法 | 10.9株 | 109.8円 | 1,200円 | +329円 | +27.4% |
| ドル · 数量累積法 | 12.0株 | 113.3円 | 1,360円 | +320円 | +23.5% | |
| 株安 | ドル · コスト平均法 | 14.6株 | 82.4円 | 1,200円 | −326円 | −27.2% |
| ドル · 数量累積法 | 12.0株 | 86.7円 | 1,040円 | −320円 | −30.8% | |
さりながら、ドル · コスト平均法に問題がある訳ではない。
株安時に「損失額」は大きくなることはあっても、「損益率」はドル · 数量累積法よりもマシである。
むしろ、株安時のドル · コスト平均法が、保有株数が最も多く、かつ平均取得単価が最も低くなるため、
プラスの期待値が実現した際には最も大きなリターンをもたらす。
ドル · コスト平均法は、株価が横ばい、株高、株安のいずれであっても、ドル · 数量累積法よりも平均取得単価はく、損益率も高かった。
しかし、実はドル · 数量累積法でもドル · コスト平均法とほぼ同じパフォーマンスを出すことができる。
表2に示したドル · 数累積法の投資総額がドル · コスト平均法と一致するように株を売買すると、表2の結果は表3に変化する。
税金や手数料を考慮しなければ、追加売買のタイミング次第で、両者は大差ない結果となることが分かる。
| チャート/方法 | 保有株数 | 平均取得単価 | 投資総額 | 損益 | 損益率 | |
| 株高 | ドル · コスト平均法 | 10.9株 | 109.8円 | 1,200円 | +329円 | +27.4% |
| ドル · 数量累積法 | 10.9株 | 110.5円 | 1,200円 | +320円 | +26.7% | |
| 株安 | ドル · コスト平均法 | 14.6株 | 82.4円 | 1,200円 | −326円 | −27.2% |
| ドル · 数量累積法 | 14.7株 | 81.8円 | 1,200円 | −320円 | −26.7% | |
既に紹介したが、資産ポートフォリオにおいて、この追加売買で資産を元の比率に戻すのがリバランスである。
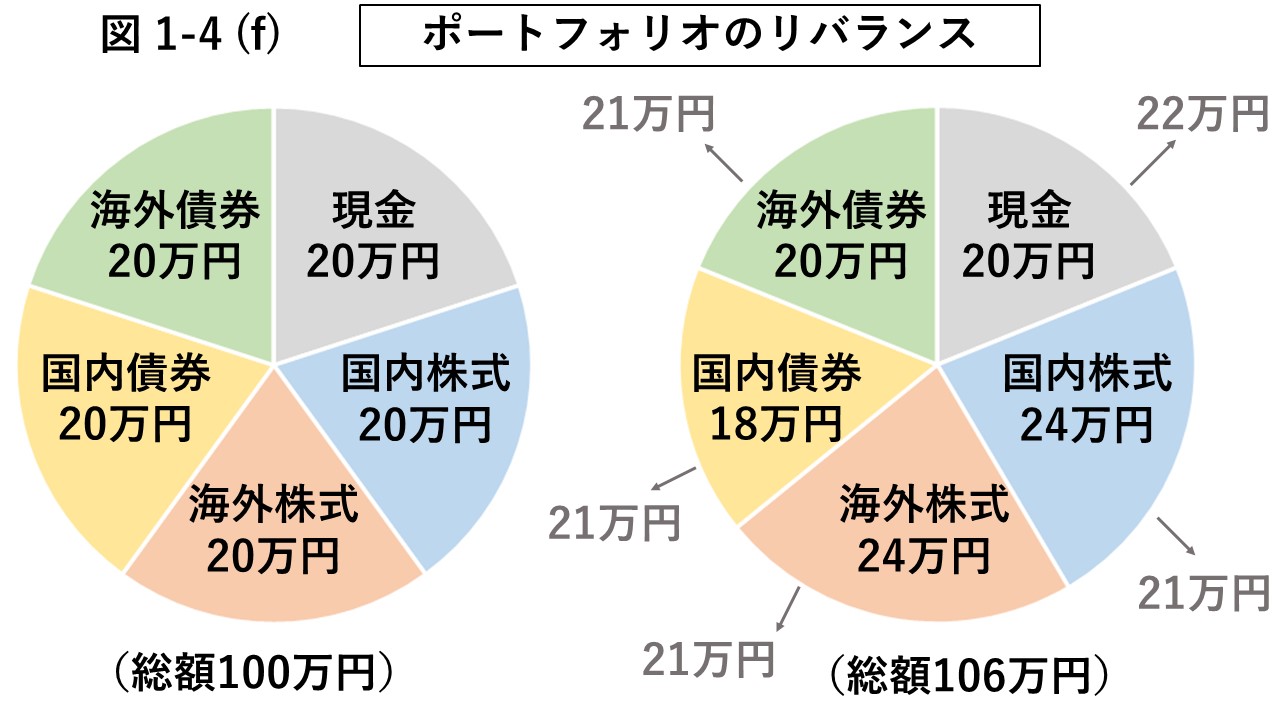
例えば、図1-4 (f)において、左のポートフォリオから国内株式と海外株式が20%上昇し、
国内債券が10%下落すると、右のポートフォリオへと変化する。
右のポートフォリオから増価した株式を売り、国内債券を購入すると、
国内債券の平均取得単価は下がり、増加した資産全体が元のバランスに戻る。
また、積立リバランスと呼ばれる方法も知られている。
積立リバランスは、いずれかの資産を売るのではなく、目標に対して低い比率の資産を買うことでバランスを取っていく方法である。
この方法では、評価益がプラスの資産を売却しないため、納税額を抑えながら複利の効果を得られる。
図1-4 (g)に、2005年1月から2021年12月まで、毎月5万円を日経平均株価に対して積立投資した場合の資産額の推移を赤線で示した。
加えて、その間の年末の日経平均株価の推移を青線で、2008年1月から同様の積立投資を開始したケースを緑線で示した。
日経平均株価に直接投資することはできないため、図1-4 (g)はフィクションに過ぎないが、
投資信託やETFなどを使っても似たような結果になったはずである。
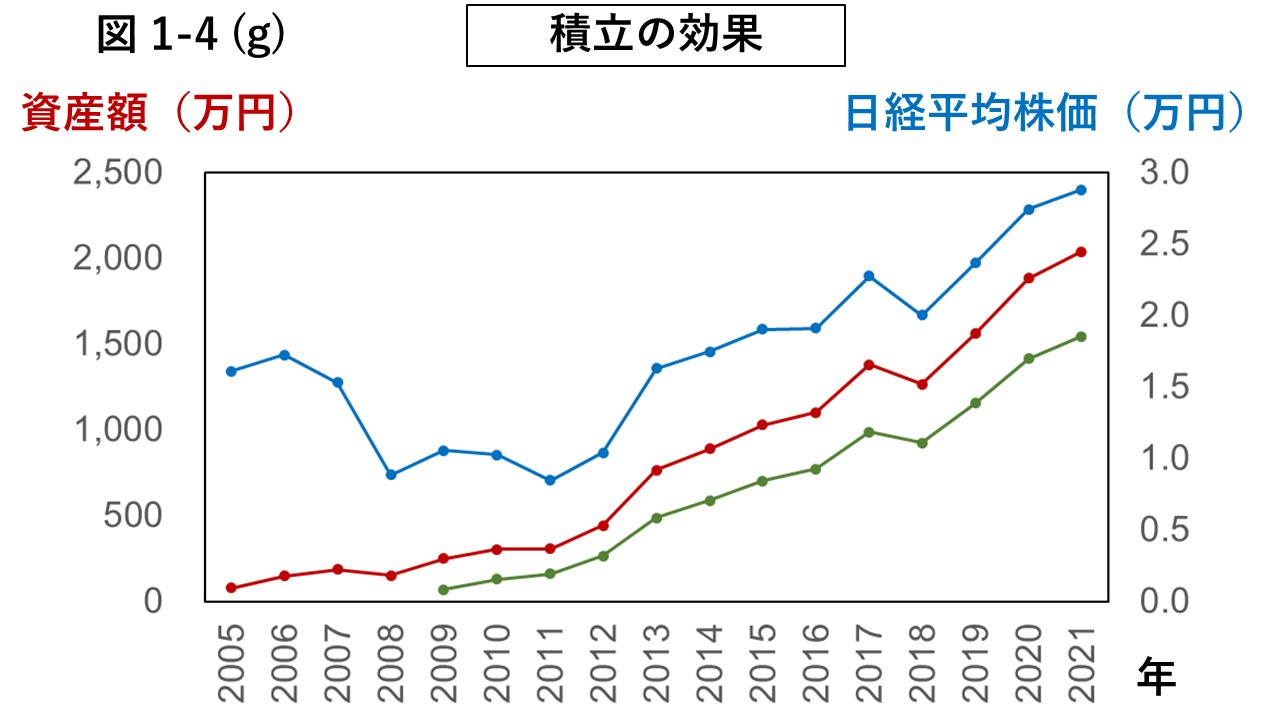
この図からは、日経平均株価は2006年から2008年にかけて大きく下落しているにもかかわらず、
資産額は大して影響を受けていないことが分かる。
その理由は、当然に損失は発生しているが、投資初期は投資金額が小さいために、積立てる金額が損失を補っているからである。
そして、相場の底である2009年1月から投資を開始した場合でも、
その資産価値は、2005年1月から投資した場合の資産価値を超えなかった。
表4に、これら2つのケースの投資総額と2021年末の資産を示した。
表4からは、2009年から投資を開始した場合、2005年から投資した場合よりもannualized ROIは高いが、最終的な資産額が少ないことが分かる。
このことは、相場の底を当てれば儲かるとは限らないことを示している。
| 投資開始年 | 投資総額 | 2021年末資産額 | ROI | annualized ROI |
| 2005年 | 1020万円 | 2038万円 | 99.8% | 4.4% |
| 2009年 | 780万円 | 1543万円 | 97.8% | 5.8% |
継続的に投資を続けると、相場が上昇したときにその恩恵をフルに受けられる。
そして、相場が上がるか下がるか分からないのであれば、投資を始めるのは早い方が有利なのである。
なぜなら、投資の期待値はそもそも上がる方向を示しているからである。
加えて、図1-4 (g)のケースでは、資産額の推移以外に、図に示されていない配当収入も期待できる。
+10%の収益率による利益と−10%の収益率による損失は、1回であれば同じだが、繰り返されると金額が異なってくる。
図1-4 (h)は、100万円が毎年10%ずつ、増加あるいは減少した場合の資産の変化を示したものである。
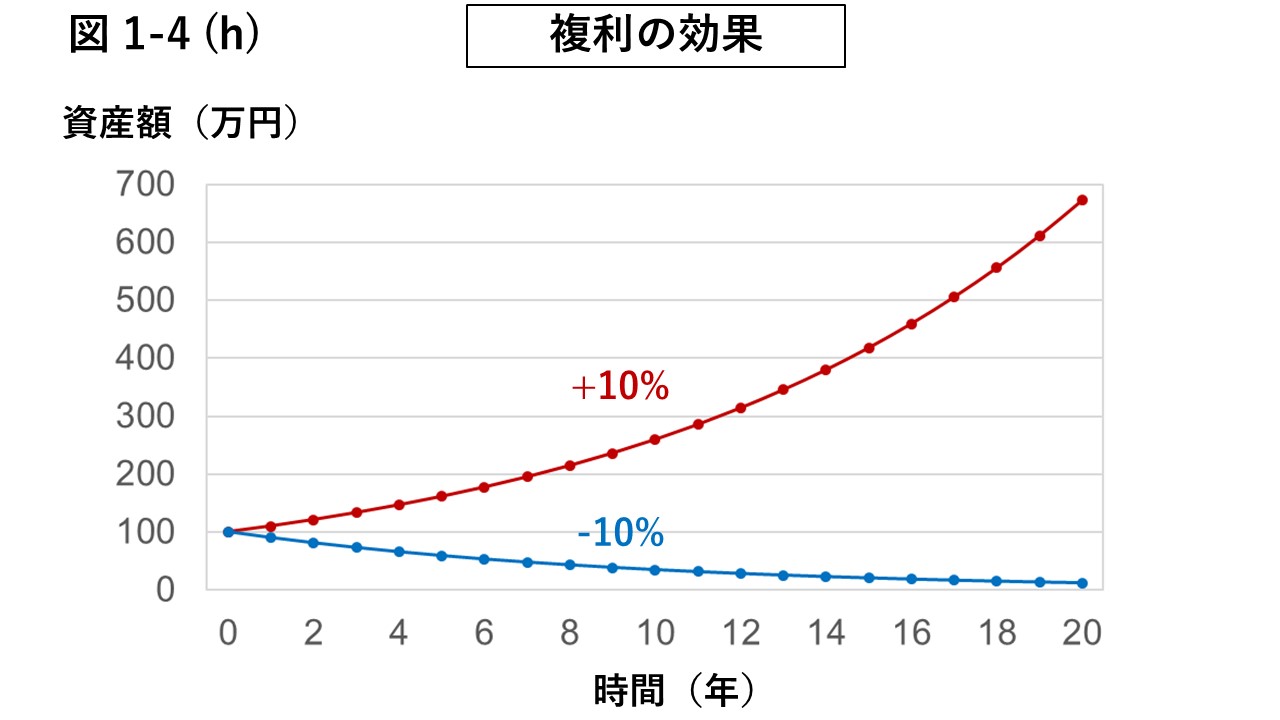
100万円の資産の20年後の価値は、毎年10%ずつ価値が増え続けたケースでは約673万円にもなるが、
毎年10%ずつ価値が減り続けたケースでも約12万円残る。
その理由は、10%の増加が2回繰り返されると21%増えるが、10%の減少が2回繰り返されても19%しか減らないからである。
このような効果は複利の効果として知られている。
ref 2
普通、複利という言葉は資産が増える場合に使われるが、本ウェブサイトでは資産が減る場合についても同様に取り扱う。
複利の効果は、普通の手法で資産を運用する上では、利益に制限はないが、損失は元本に限られることを示している。
複利の効果は一見素晴らしいことのように思えるが、資産が常に増え続けない限り、図1-4 (h)の赤線のような幸運は訪れない。
図1-4 (i)に、100万円の資産の価値が、10%ずつ増える又は減ることが繰り返された場合のシミュレーションを示した。
このケースでは、1度損失を出すと、概ね2年前の資産額に戻ってしまうことが分かる。
加えて、同じ損益率が同じ回数繰り返されると、資産額は同じにはならず、僅かに損をする。
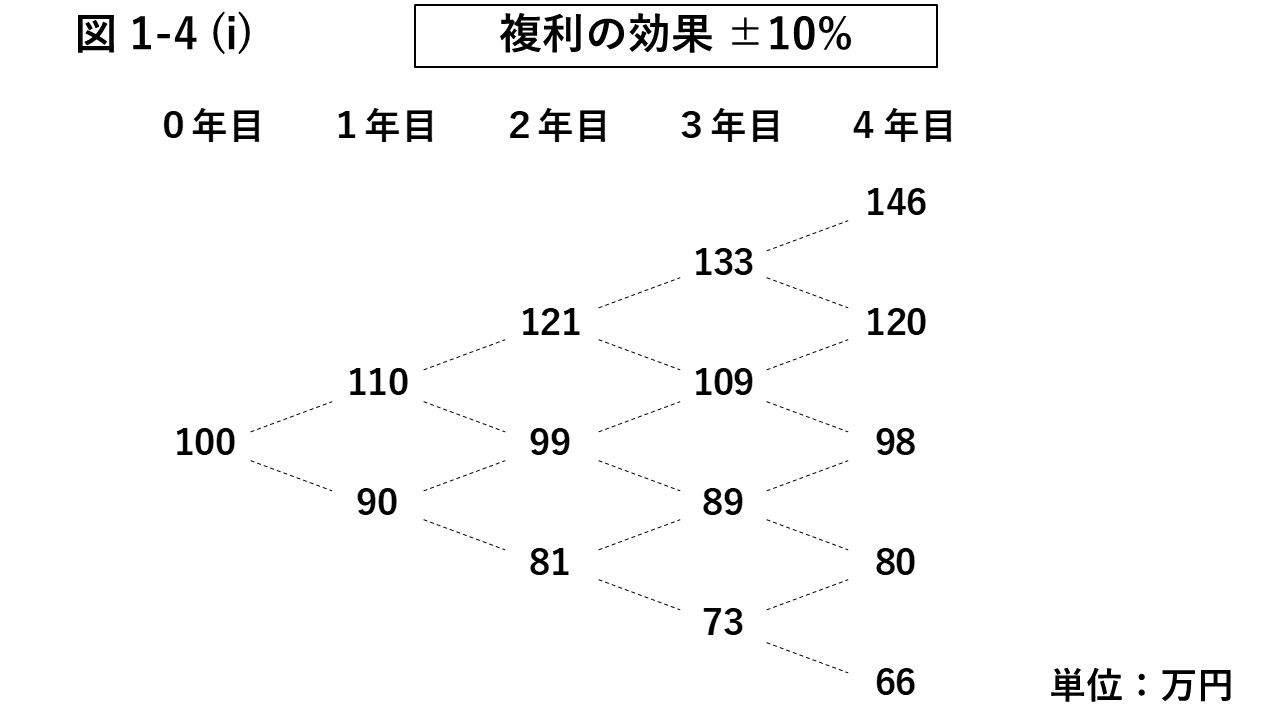
同じ変化率が続く限り、複利の効果はより一般化して考えることができる。
図1-4 (j)に、元本Pが、±\(r\)%の増減率を繰り返した場合の図式を示した。
図では、+\(r\)%の変化を\(r_{+}\)で、−\(r\)%の変化を\(r_{-}\)で表している。
\(r_{+}\) が続くほど年の経過とともに資産価値は右上へ変化し、\(r_{-}\)が続くほど年の経過とともに資産価値は右下へ変化する。
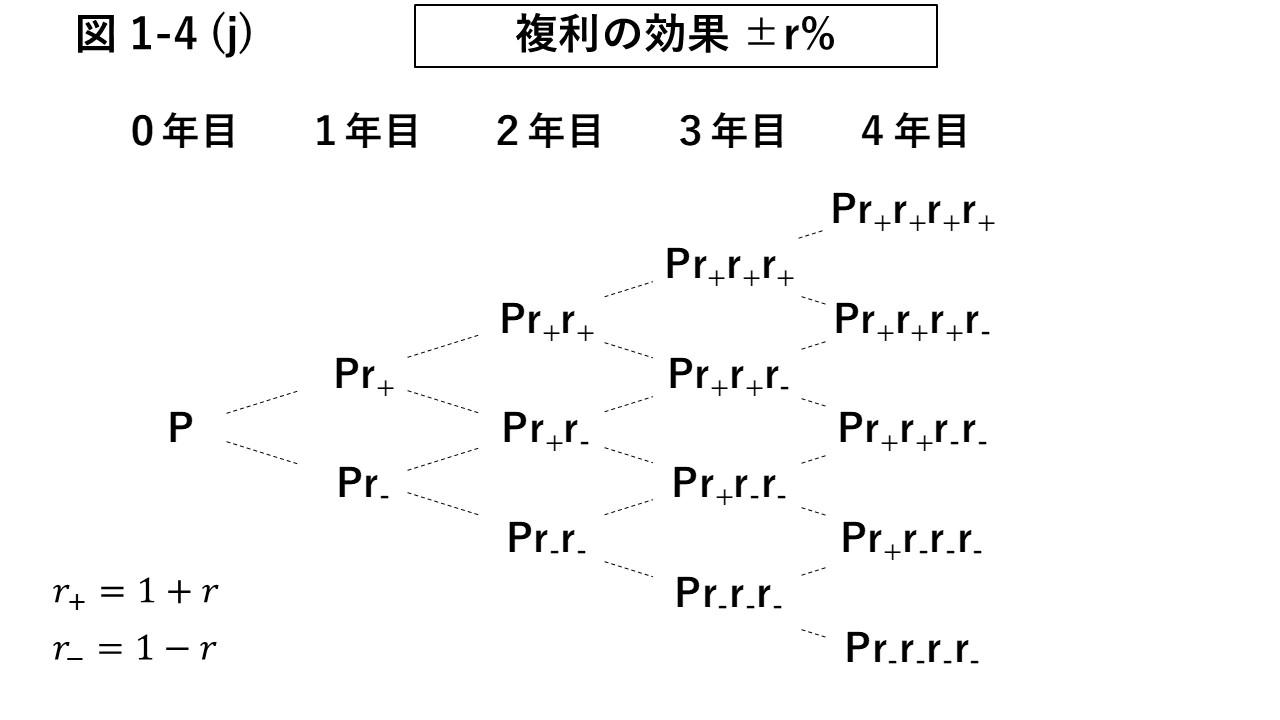
\(r_{+}\) が積み重なるほど、複利の効果により資産は加速度的に拡大する。
しかし、一度 \(r_{-}\) が付くと、それまでに増加した資産の全額に対して損失が出ることが分かる。
そして、同じ増減率を同じ回数繰り返したときに損失がでるのは、式(2)の \(r^{2}\) の分がマイナスされるからである。
しかし、このことは投資が不利なゲームであるという意味ではない。
図1-4 (j)の図式が示しているのは、正確には、50%の確率で勝ち負けが決まり、増減率も同じであるギャンブルに利益を上乗せしていった場合の結果の予想図である。
ここまでに既に述べたように、投資は期待値がプラスの、勝率あるいは増減率に対して底上げ効果が見込まれるゲームである。
加えて、投資家は利益を上乗せする必要もない。
そのため、資産を適切にマネジメントすれば、投資は利益に上限の無いゲームであり、かつ全財産を失うようなゲームではない。