本ページでは、投資のリスクの意味およびリスクとリターンの関係を説明し、期待値と分散の考え方について紹介する。
投資のリスクという言葉があるが、その意味には不明な点が多い。
投資におけるリスクとは、一般的にはリターンの振れ幅のことと考えられている。
ref 1
そして、投資のリスクの説明によく用いられるのが、ハイリスク · ハイリターンという言葉と、
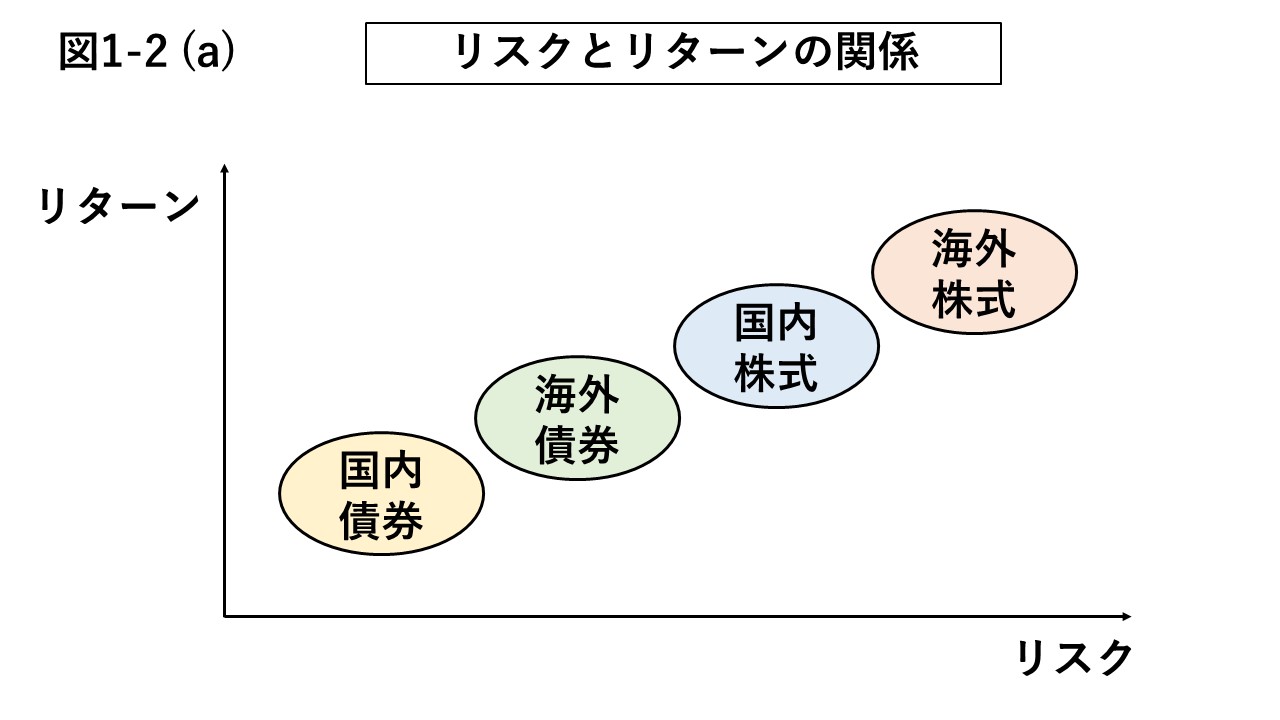
図1-2 (a)に示したリスクとリターンの関係図である。
一方で、リスクには種類があるとされる。
ref 2
金融商品によって、以下のような様々なリスクの種類が指摘されている。
|
|
しかし、実際にはリスクの数はこれほど多くはない。
なぜなら、いずれのリスクも価格変動と関係しており独立していないからである。
ここで挙げられた価格変動リスク以外のリスクに冠された名詞は、いずれも価格変動の原因を表すものでしかない。
問題は、リターンの振れ幅という意味でのリスクと、この価格変動リスクが同じものかどうかである。
リスクがリターンの振れ幅であれば当然その定まった中心があるはずだが、価格変動であればその中心の存在を認識できない。
経済活動は自然現象ではなく、資産価格に確実な中心は定まり得ない。
そのため、リターンの振れ幅とされるリスクは過去から現在のことを表しており、
価格変動とされるリスクは現在から未来のことを表していると考えられる。
親が子に「車にぶつかると危険だ」と教える場合、未来に対して危険だ言っているが、
危険であるという認識は過去に形成されたものである。
したがって、「投資にはリスクがある」と言われた場合、未来に対してリスクがあると言っているが、
そのリスクは過去の出来事に由来していると解釈できる。
一方で、リターンの振れ幅と価格変動という言葉の共通点は、価格が上がるとも下がるとも言っていないことである。
すなわち、一般に考えられているリスクと異なり、投資におけるリスクは悪い方のことばかりを意味していない。
よって、投資のリスクの正確な意味は、 「どのような資産でも過去にある程度の価格変動があり、投資すると、今後も資産価格が上下することがある。」という解釈となる。
一見当然のようだが、過去にどの程度の価格変動があったのかについて知らなければ、そのリスクが認識できない。
確率を分布で考えると、図1-2 (a)で示した
リスクとリターンの関係をイメージしやすい。
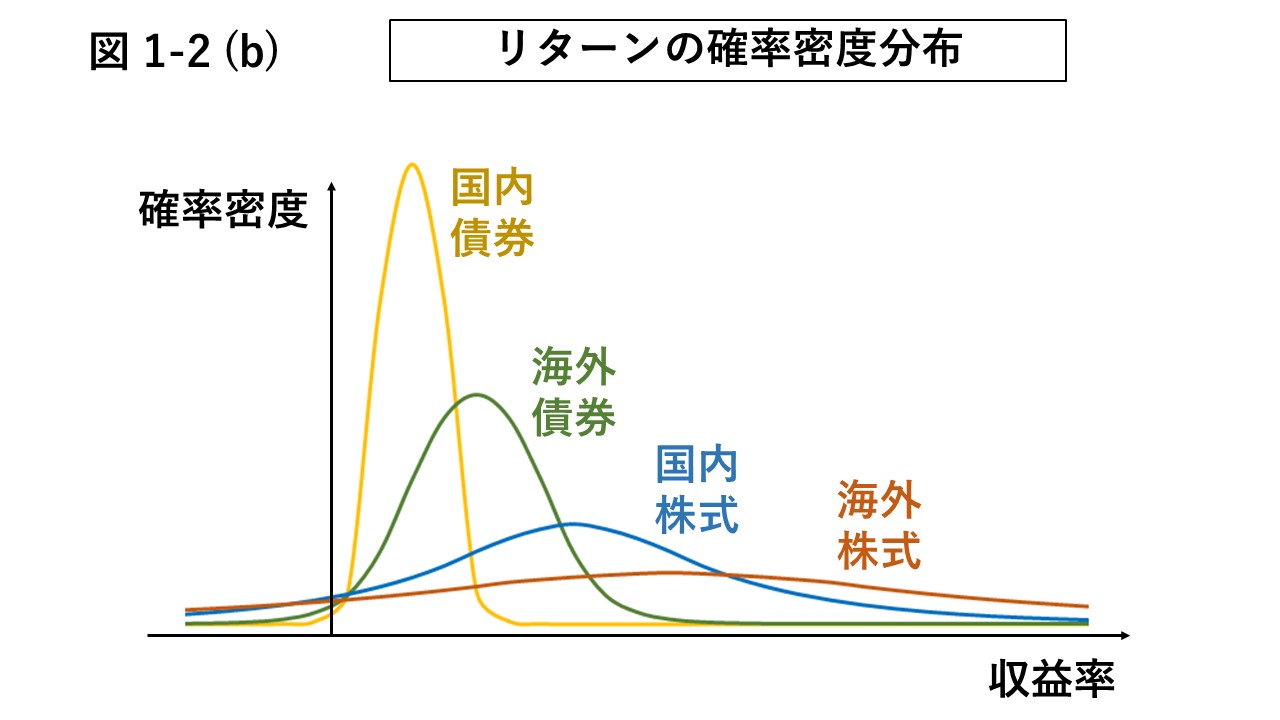
図1-2 (b)は、資産クラス毎の過去の値動きのイメージを示したものである。
各資産の収益率 (リターン) の分布において、その期待値が期待収益率 (期待リターン) であり、
収益率のバラつき (リターンの振れ幅) がリスクである。
言い換えると、分布の中央が位置する横軸の目盛りが期待収益率であり、分布の横幅がリスクである。
株式の期待収益率が5–10%という場合、その数字はおそらく年間の期待収益率を表しており、 図1-2 (b)における国内株式、海外株式の分布の中央がその程度であることに相当する。
投資に関してまず理解が必要なのは、図1-2 (b)に示した4つの資産は、
歴史的 (少なくとも1952年以降) にリターンがプラスであったことである。
このプラスの期待値こそが、投資がギャンブルと区別される所以でもある。
一方で、リスクは標準偏差 (σ) と呼ばれる統計値で表現されることが多く、株式では25%程度とされる。
しかし、期待値から±1σの範囲 (±25%) はデータの約68%しか含んでおらず、
標準偏差の値よりも分布の広がり (リスク) は大きい。
すなわち、±1σ範囲外の出来事は、約1/3の確率で起きていたことになる。
ここで、図1-2 (c)に示した奇妙なサイコロを振るゲームについて考えてみる。
1–6の目が上に出る確率は、それぞれ過去の統計から分かっており、図に示した通りである。
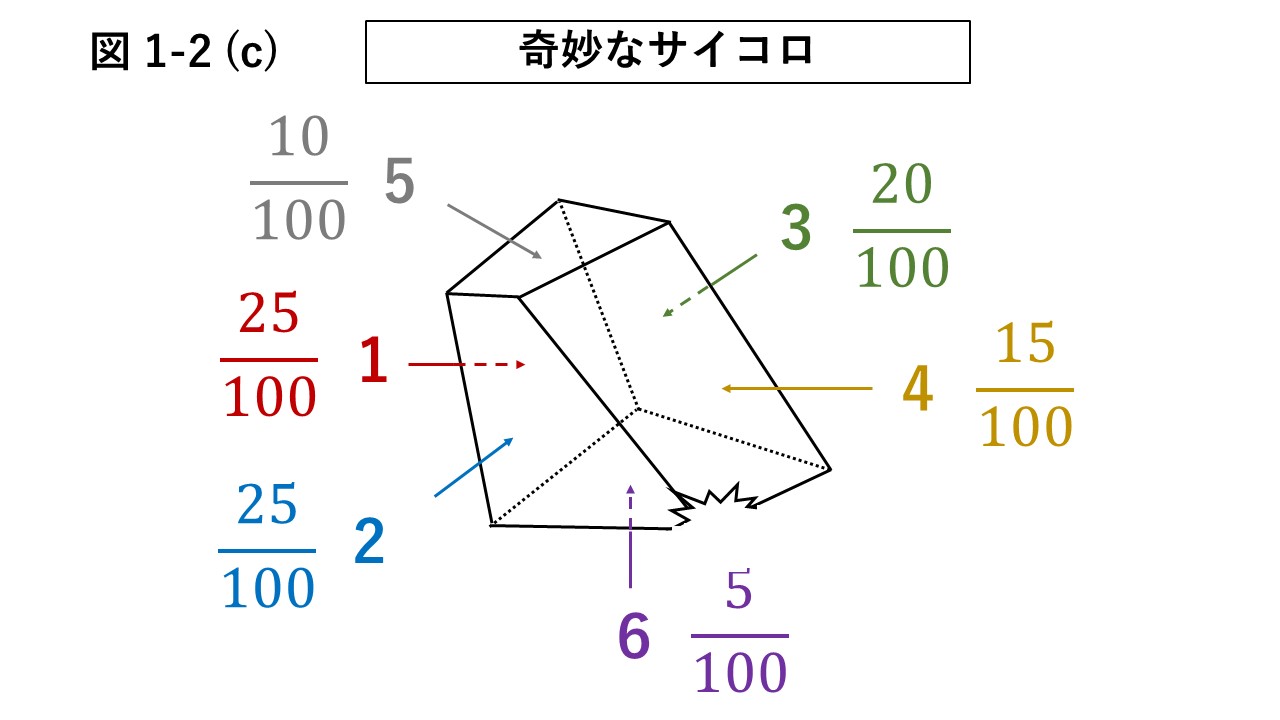
ゲームは3つで、賭け金はいずれのゲームも100円である。
サイコロを振るのは週に1回で、その際に選択できるゲームは1つだけとする。
各ゲームにおけるサイコロの目に対するリターン額および期待値と分散は、下表にまとめている。
ゲーム3は、ゲーム1とゲーム2に同時に50円ずつ賭けて払戻額も半分ずつになるルールである。
いずれのゲームも期待値はプラスであり、投資の条件を満たしている。
| サイコロの目 | 確率 | リターン | ||
|---|---|---|---|---|
| ゲーム1 | ゲーム2 | ゲーム3 | ||
| 1 | 25/100 | 110円 | 120円 | 115円 |
| 2 | 25/100 | 100円 | 100円 | 100円 |
| 3 | 20/100 | 100円 | 80円 | 90円 |
| 4 | 15/100 | 100円 | 130円 | 115円 |
| 5 | 10/100 | 100円 | 140円 | 120円 |
| 6 | 5/100 | 90円 | 70円 | 80円 |
| 期待値 | 102円 | 108円 | 105円 | |
| 分散 (標準偏差) | 37円 (6.1円) | 657円 (25.6円) | 217円 (14.7円) | |
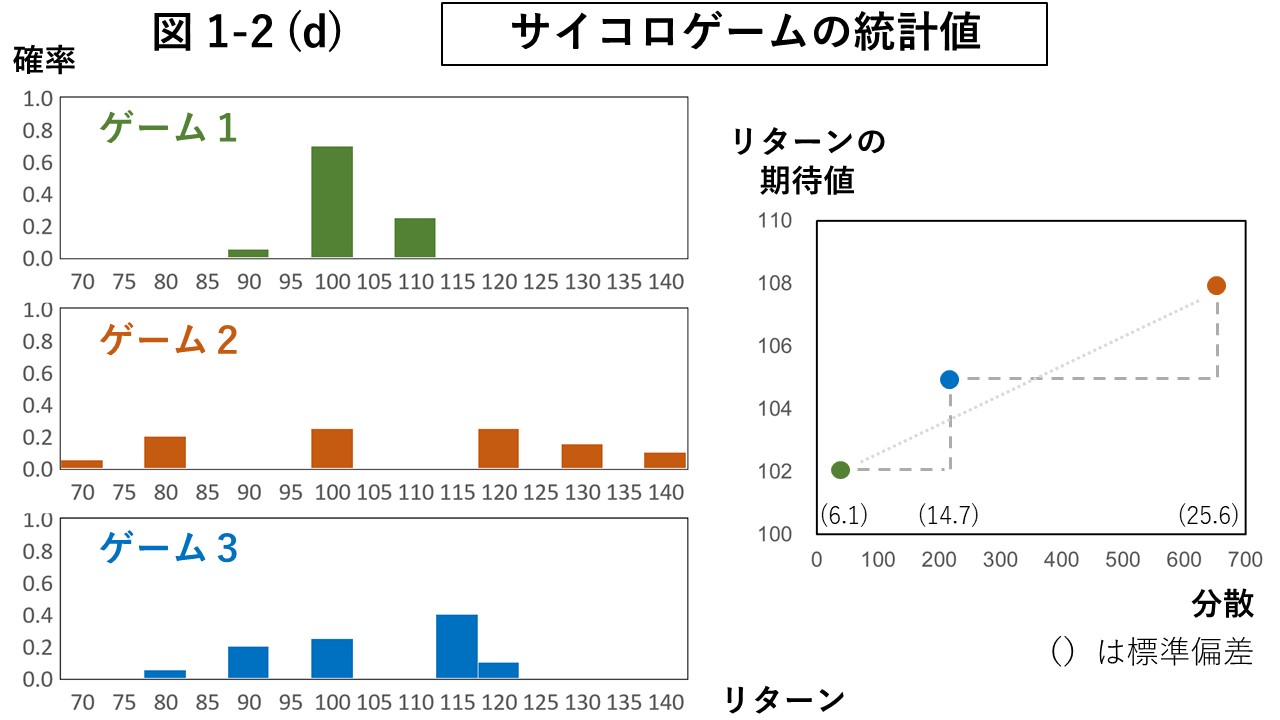
そして、この表の数字をグラフ化したものが以下の図1-2 (d)である。
ゲーム1では、大儲けしないが、大損もしない。
ゲーム2では、大儲けすることもあるが大損することもある。
ゲーム3は、ゲーム1とゲーム2に半額ずつ賭けただけだが、損をする確率が減った割には、プラスのリターンが大きいように見える。
どのゲームに賭けるのが最も良い選択なのだろうか?
最も期待値が高いのはゲーム2である。
大数の法則が成り立つならば、試行回数が増えるほどリターンは期待値に近づく。
すると、最も儲かり、元本を失う可能性はほとんど無いのではないだろうか?
問題は何回試行を繰り返せるのかである。
仮に1000回試行する場合、試行には10万円を要し、週に1回の試行では1年間に52回しかサイコロを振れない。
一方で、十分な回数の試行ができない場合、期待が実現する保証はない。
分散 (標準偏差) の意味するところは起き得る結果の幅であり、
その幅に相応な試行回数が無ければ結果の平均が期待値に収束しないからである。
結局、どのゲームに参加するべきかは、試行回数と関係がありそうである。
試行回数を多くできるのであれば、期待値の高いゲーム2が有利である。
ただし、期待が実現するまでゲームオーバーにならないことが条件である。
試行回数が少ないのであれば、分散の低いゲーム1が無難である。
こちらはかなりの確率で期待値周辺の結果が起きるため、大敗せずに手堅く稼ぐことができる。
そして、ゲーム3では、期待値に対して分散が有利になっているため、 比較的少ない試行回数で、そこそこに高いリターンが期待できる。
図1-2 (b)に示した資産クラス毎のリターンの確率分布と、
図1-2 (d)に示した奇妙なサイコロのゲームにおけるリターンのヒストグラムは、
率と額という点で異なるが、その意味合いはほぼ同じである。
しかし、サイコロゲームと投資では、重大な違いがある。
サイコロゲームの期待値と分散は1回の試行を積み重ねて得られた値であるが、
各資産の期待収益率 (リターン) と分散は、大抵の場合、過去の年末と翌年末の資産価格から得られた値である。
そのため、投資における期待収益率と分散には、年末と年始の間により大きな価格変動があることが考慮されていない。
また、サイコロのゲームでは試行毎に払い戻しがあるが、投資では売却しない限り賭け金が膨らんでゆき、その投資されたお金は当面返ってこない。
結果として、投資におけるプラスあるいはマイナスのリターンは想定よりも大きなものとなり、
そのリターンは大抵の場合、試行1回分のキャッシュに対してではなく、積み上げたキャッシュに対するものになりがちである。
とはいえ、期待値がプラスのゲームは投資以外にない。
過去の結果は未来を確約しないが、十分に長期のデータからプラスの期待値が得られているのであれば、投資する価値は十分にある。
期待値に収束する保証はないが、投資の期待値がプラスであることについては確からしい根拠がある。
トマ · ピケティが『21世紀の資本』で示した「r > g」と、過去の着実な経済成長である。ref 3
また、各資産の期待収益率と分散が示しているものは、それらの資産の過去の値動きであって、投資家のリターンではない。
投資では、自分の賭け方次第で、自らの資産のリターンやリスクを変えることができる。
自らの資産のリターンを増やし、リスクを下げるためには、過去のデータだけではなく、投資の仕組みやテクニックを知る必要がある。