本ページの目的は、企業や株式の分析に用いられる指標のうち、株式市場の評価に関する指標について解説することである。
時価総額(Market capitalization)とは、企業が発行した普通株式の総価値である。
しばしば、Market Capと呼ばれる。
時価総額は、平たく言えば、株式市場におけるその株式の存在感を表す指標である。
時価総額は株価に発行済株式数を掛けることで計算できる。
時価総額 = 株価 × 発行済株式数
時価総額は上の式で求めることができるが、時価総額とは何で決まるのだろうか?
株価が上がれば時価総額が増加するのは理解できる。
しかし、発行済株式数が増加すれば時価総額は上がるのだろうか?
まずは、利益の観点から時価総額について議論する。
株価は、その1株当たり利益(EPS)とその倍率(PER)の積で表すことができる。
そして、EPSは純利益を発行済株式数で割った値である。
株価 = EPS × PER
EPS =
当期純利益
発行済株式数
この式を用いて時価総額の式を書き直すと、以下の式になる。
時価総額 = = 当期純利益 × PER
この式は、時価総額は純利益の影響を受けるが、発行済株式数の影響を受けないことを示している。
そして、利益の観点からは、時価総額とは純利益と将来に対する期待を反映したものと捉えることができる。
つまり、時価総額とは普通株式の市場規模であり、企業の純利益と将来に対する期待はその規模を形成する要因であると考えられる。
この式の両辺を発行済株式数で割ると、元の株価の式に戻る。
株価 = EPS × PER
つまり、発行済株式数が同じであれば、時価総額と株価は比例関係にある。
しかし、株価は1株当たり利益に対応した価格であり、発行済株式数が変化した場合、その影響を受ける。
例えば、株式分割により発行済株式数が2倍になった場合、理論上の株価は半分になる。
しかし、株価が半分になったとしても、株式数が増えるため、株主の所有する株式の総額は分割の前後で変化しない。
そして、これらの普通株主の所有する株式の価値の合計である時価総額も分割の前後で変化しない。
このように、同じ企業の株価であっても、株価は発行済株式数次第で水準が変化する。
加えて、株価の水準は、上場した時点で企業によってまちまちである。
そのため、株価は株式市場におけるその株式の存在感を表す指標としては不適切である。
一方で、時価総額は発行済株式数で変化しない。
そして、時価総額は企業の利益を反映している。
そのため、市場における異なる企業の株式の存在感を考える上では、株価よりも時価総額の方が適切である。
とはいえ、通常、株価チャートにおける株価の推移は、時価総額の推移と形は同じである。
時価総額のチャートは一般的でないため、投資家は時価総額の変化を株価の変化を通して見ることになる。
株価が発行済株式数の影響を受けるにもかかわらず、株価と時価総額の推移が同じ形になるのは、株価チャートが必要に応じて修正されるからである。
例えば、株式分割の場合、それによって株価が下がったとしても、分割以前の株価が新たな株式数によって修正される。
株式市場では、企業は時価総額の大きさに応じて、Large Cap、Mid Cap, Small Capのように分類して呼ばれる。
Large Cap銘柄は、純利益が大きい、かつ/または、発行済株式数が多い銘柄である。
一方で、Small Cap銘柄は、純利益が小さい、かつ/または、発行済株式数が少ない銘柄である。
ここまで時価総額に発行済株式数は影響しないとして話を進めてきたが、それは利益の観点からであった。
しかし、現実には発行済株式数は時価総額に影響を与え得る。
流動性の高い銘柄は、市場での売買で値が付きやすく、株価は安定する傾向にある。
一方で、流動性の低い銘柄は、市場で指値が離散的になりがちであり、売買自体が成立しにくく、株価も変動しやすい。
そのため、流動性リスクの観点から、発行済株式数の多い銘柄は、少ない銘柄よりも選好されやすい傾向がある。
特に機関投資家は扱う金額が大きいため、流動性の低い銘柄を取り扱うことは少ない。
また、時価総額の大きい銘柄は、ETFや投資信託にも組み入れられやすい。
そのため、投資家によってその銘柄が選ばれなくても、ETFや投資信託の購入を通じて株価が下支えされる面がある。
しかし、流動性リスクは企業の単独オーナーにとっては問題とならない。
そして、時価総額の大きな銘柄が意図せず下支えされることは、市場によるフェア・バリュー形成を阻害する要因にもなり得る。
見方を変えれば、Small Cap銘柄は、市場に注目されていないため、利益に対して適正な株価を形成しないことがままあり、株価も動きやすい。
そのため、Small cap銘柄は、株価が上がる時にはLarge Cap銘柄よりもはるかに高いパフォーマンスを示すことがある。
そこで、個人投資家にとってlarge Cap銘柄とSmall Cap銘柄を両方取得することは、分散投資の1つの選択肢になり得る。
ところで、企業の全株式の取得は、その企業の単独オーナーになることを意味する。
そのため、全株式の価格である時価総額は企業の買収金額に相当する費用と考えられがちである。
しかし、時価総額は、普通株式の総価値であり、貸借対照表の自己資本の部分に対する評価額である。
企業を買収する場合、貸借対照表を丸ごと購入することになるため、自己資本以外の評価額も加味して上積みを支払う必要がある。
つまり、時価総額は企業の買収に要する最低金額である。
事業価値(EV:Enterprise Value)とは、事業から将来生み出されるキャッシュフローの割引現在価値である。
以下、事業価値の説明と共に、類似の概念である企業価値(CV:Corporate value)についても説明する。
時価総額のセクションで、企業の買収において、時価総額に対して上積みが必要であると述べた。
企業価値とは、時価総額に、その上積みとして有利子負債を加えた金額である。
CV = 時価総額 + 有利子負債
有利子負債は、短期長期を問わず利息を払う必要のある債務のことである。
本ウェブサイトでは、話を簡単にするため、時価総額に対する上積みとして、有利子負債のみを用いる。
細かくは、有利子負債以外にも上積みが必要なケースがある。
例えば、優先株や非支配株主持分のような、普通株式の株主以外の資金の出し手に対する上積みである。
このような普通株主以外の資金の出し手に対しては、その価値に対応する金額を支払う必要がある。
CVの意味するところは、以下のようなものである。
簿価貸借対照表は、左側は事業性資産と非事業性資産に、右側は事業性負債、有利子負債、純資産に分けられる。
事業性資産は、事業に関連する受取手形及び売掛金、商品及び製品のような流動資産や、有形・無形の固定資産のことである。
非事業性資産は、現金及び預金に加え、売買目的有価証券、遊休土地のような、事業のCFと直接関係なく売りやすい資産のことである。
事業性負債は、支払手形及び買掛金、賞与引当金のような、事業に関連する運営の過程で生じる負債のことである。
このように資産、負債を分類したうえで、純資産のうち、自己資本を時価総額で置き換えると、図2-5-1 (b)に示すように、簿価からの資産の増加分をのれんと見なすことができる。
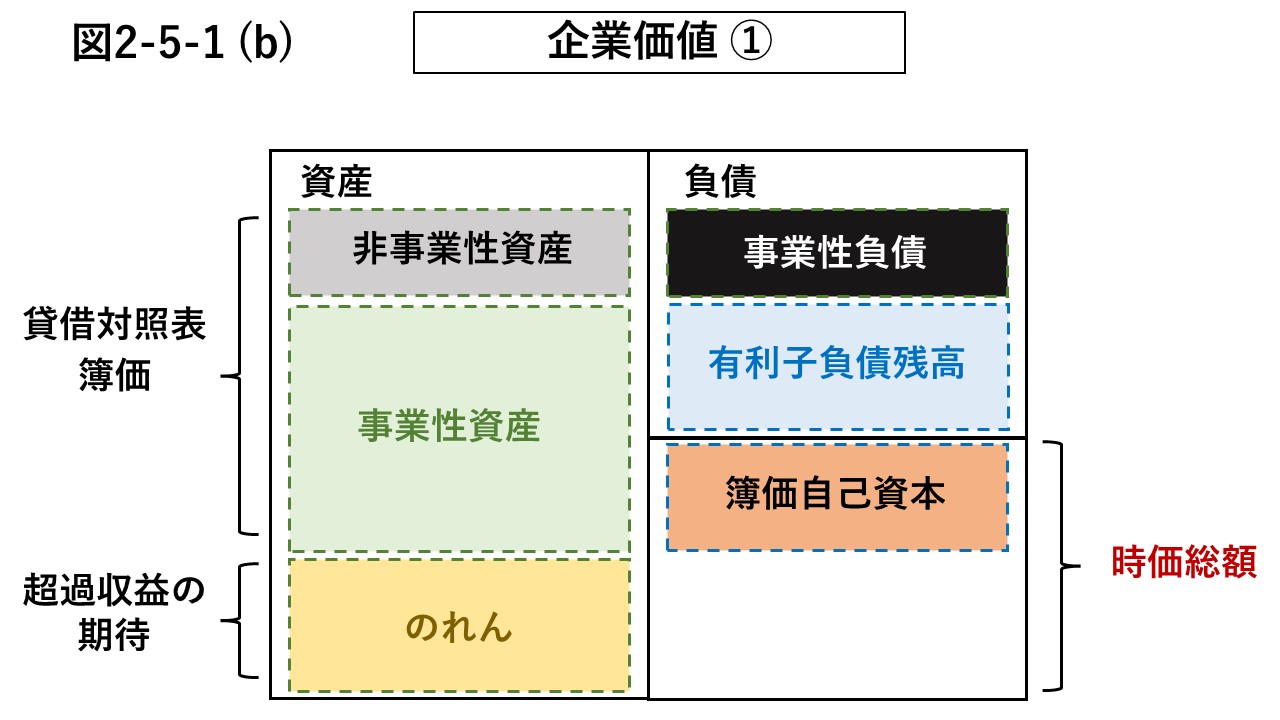
続いて、図2-5-1 (c)に示すように、事業性負債を事業性資産の流動資産で相殺すると、貸借対照表の左側には事業性資産としておおむね固定資産が残る。
このとき、貸借対照表の右側は時価総額と有利子負債となっており、CVの式の右辺と一致している。
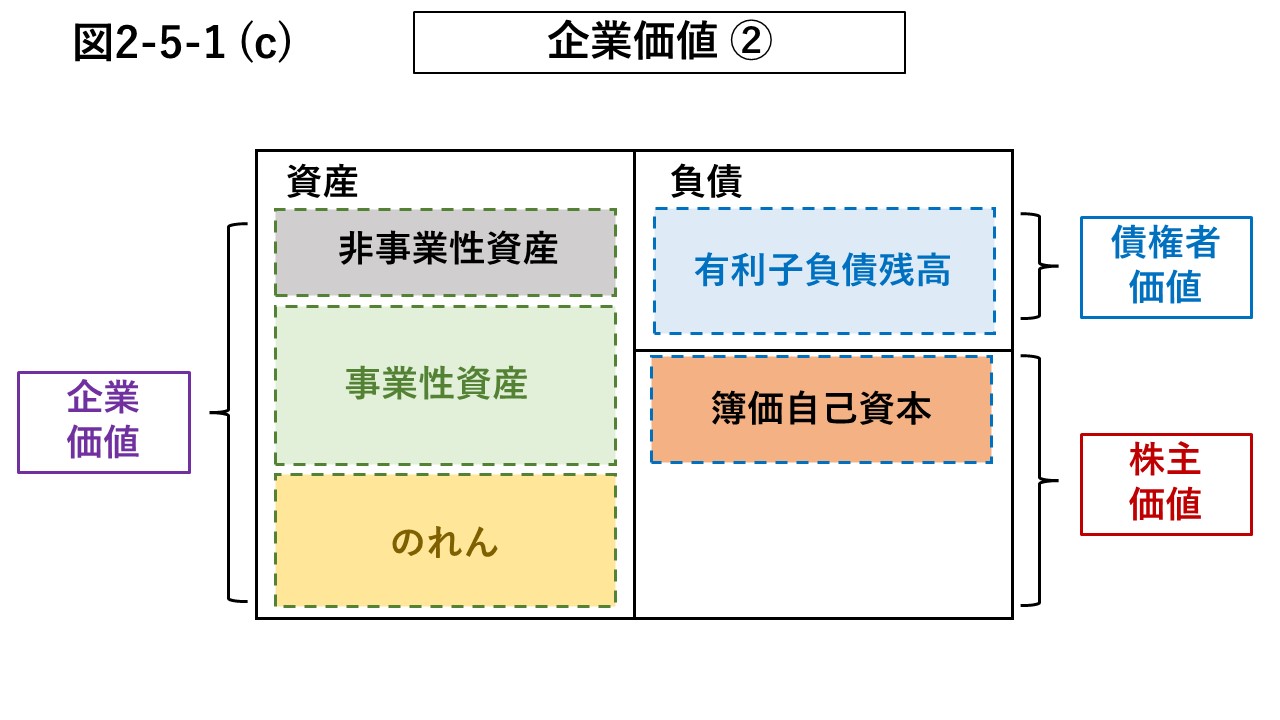
CVとは、図2-5-1 (c)の左側に示された、事業性資産および非事業性資産にのれんを加味した価値のことである。
そして、右側の有利子負債の部分が債権者にとっての価値(債権者価値)、時価総額の部分が株主にとっての価値(株主価値)である。
要するに、CVとは、債権者と株主の両者に帰属する価値であり、企業の買収金額に相当する。
ところで、企業を買収する側にとって、欲しいものは企業ではなく事業ではないだろうか?
事業を買収する場合、図2-5-1 (c)の左側の、ビジネスと関係のない非事業性資産は不要である。
事業価値とは、CVからこの非事業性資産を除いたものである。
事業価値(EV)は、以下の式で表される。
EV = 時価総額 + 有利子負債 − 非事業性資産 = 時価総額 + ネット有利子負債
ネット有利子負債は、有利子負債と非事業性資産の差額である。
図2-5-1 (c)から、有利子負債の一部を非事業性資産で相殺すると、図2-5-1 (d)となる。
これらを相殺することは、買収後に非事業性資産によって有利子負債の一部を返済することに相当する。
図2-5-1 (d)の右側には、時価総額とネット有利子負債が残り、EVの式と一致している。
CVの金額で企業を買収し、非事業性資産によって有利子負債の一部を返済すると、EVが残る。
要するに、EVは、事業のネット買収金額に相当する。
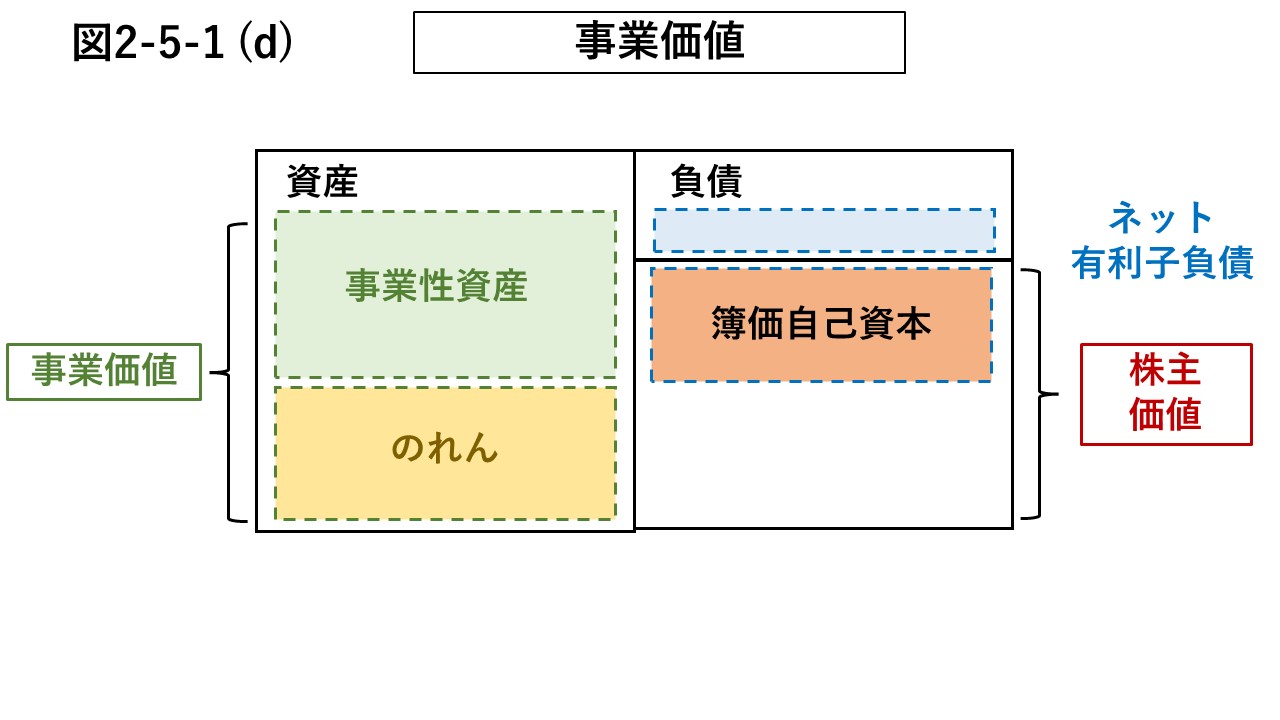
EVとは、図2-5-1 (d)の左側に示された、事業性資産にのれんを加味した、ビジネスでキャッシュを生み出す力に対する評価のことである。
すなわち、冒頭で述べたように、EVとは事業から将来生み出されるキャッシュフローの割引現在価値に相当する。
ここまでの説明は、時価総額を株主価値とし、それを基に事業価値を評価する方法(マーケットアプローチ)に沿ったものである。
事業価値の評価方法は他にもいくつか存在し、その1つはインカムアプローチと呼ばれる。
インカムアプローチでは、事業価値は、DCF法により、事業が将来生み出すFCFの割引現在価値として直接的に算出される。
割引キャッシュフロー法(DCF法 : Discount Cash Flow 法)は、 投資対象の企業あるいは株式が将来生み出すキャッシュフローの割引現在価値を計算する方法である。
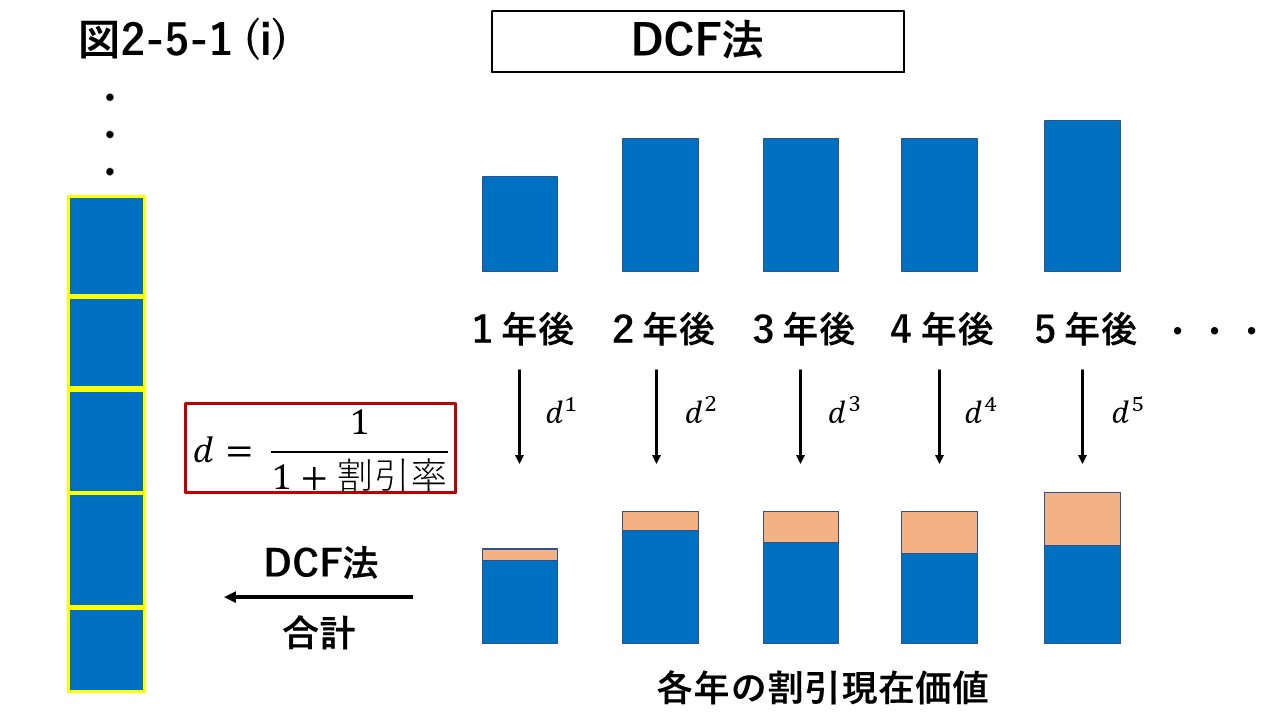
割引現在価値は、将来のキャッシュフローを現在に割り戻せば得られる。
図2-5-1 (i)に示すように、DCF法では、各年のキャッシュフローを現在価値に割り戻して合計することで、将来生み出すキャッシュフローの割引現在価値を求める。
ちなみに、ここでいうキャッシュフローとは、企業のCFでなくとも、利息や配当、企業のFCFなど、お金のフローになるものであれば何でもよい。
キャッシュフローにFCFを用いた場合、DCF法で得られる解は、事業価値(EV)を表すことになる。
DCF法では、割り引かれる対象と割引率が必要である。
ここでは、割り引かれる対象を\(T\)、割引率を\(r\)として、DCF法で用いられる式を導出する。
ただし、\(0 \lt\ r\) である。
(1) 割り引かれる対象 \(T\) (FCFや配当)が \(n\) 年間一定だと仮定した場合、将来生み出されるキャッシュ・フローの割引現在価値 \(S_{n}\) は、式 (4-1) で表される。
式 (4-1) の両辺に \((1 + r)\) をかけると、②式になる。
そして、式 (4-2) から式 (4-1) を引くと、以下の式(4-A)になる。
この式(4-A)を、n年間ゼロ成長モデルと呼ぶことにする。
式(4-A)において、\(n\ \to\ \infty\) とした場合、右辺第2項はゼロに収束するので、\(S_{\infty}\) は式(4-B)で表される。
この式(4-B)を、永久ゼロ成長モデルと呼ぶことにする。
(2) 割り引かれる対象 \(T\) が、\(k\) 年目以降( \(k + 1\) 年目から)、\(n\) 年間一定だと仮定した場合、将来生み出されるキャッシュフローの割引現在価値 \(S_{k+1 ~ \infty}\) は、
式(4-B)の \(S_{\infty}\) から、式(4-B)において \(n = k\) とした \(S_{k}\) を引くことで得られる。
この式(4-C)を、減速永久ゼロ成長モデルと呼ぶことにする。
(3) 割り引かれる対象 \(T\) が毎年 \(g\) %成長する場合、n年目までに生み出されるキャッシュフローの割引現在価値 \(S_{n}\) は、式 (4-3) で表される。
式 (4-3) の両辺に \((1+r)/(1+g)\) をかけると、式 (4-4)になる。
そして、式 (4-4) から式 (4-3) を引くと、以下の式 (4-D) になる。
この式(4-D)を、n年間g成長モデルと呼ぶことにする。
式(4-D)において、\(r \lt\ g\) であれば、\( (1 + g)T/(r - g) \ \lt\ 0 \) となる。
そして、\(n\ \to\ \infty\) のとき、\( (1 + g)^n / (1 + r)^n \to\ \infty \) となる。
そのため、\(r \lt\ g\) であれば将来発生するキャッシュフローの割引現在価値\(S_{\infty}\) は \(+\infty\)に発散する。
一方で、\(g \lt r\) であれば、\(n\ \to\ \infty\) のとき、
\(
(1 + g)^n / (1 + r)^n
\to\ 0
\)
となるので、\(S_{n}\) は以下の式 (4-E) に収束する。
この式(4-E)を、永久成長モデルと呼ぶ。
ちなみに、\(g = 0\) の場合、式 (4-D) は式 (4-A) と、式 (4-E) は式 (4-B) と同じになる。
ここでは、DCF法を用いて事業価値(EV)を算出する例を示す。
割り引かれる対象 \(T\) を各年のFCFとし、割引率 \(r\) にはWACCを用いる。
FCFが30億円、株主資本(時価):有利子負債=2:1の企業を想定する。
株主資本コストが8%、負債コストが0%、実効税率が30%であれば、その企業のWACCは5.3%である。
以下、この企業でDCF法の概要を説明する。
当該企業が成長の見込みは無いものの、FCFは安定していて永久に現状維持だと仮定した場合、永久ゼロ成長モデルの式 (4-B) を用いる。
すなわち、この企業の事業価値(EV)は566億円と算出される。
当該企業のFCFが、10%の成長を10年間継続し、その後、安定企業となるケースを考える。
この場合、はじめの10年間についてはn年間g成長モデルの式 (4-D) を、以降は減速永久ゼロ成長モデルの式 (4-C) を用いる。
(1) はじめの10年間
よって、はじめの10年間に期待されるFCFの割引現在価値の総和は、384億円である。
(2) 11年目以降
11年目からは成長しないため、まず10年目のフリーキャッシュフロー \(FCF_{10}\)を求める。
そして、この \(FCF_{10}\) を式 (4-C) の\(T\) に当てはめる。
よって、11年目以降に期待されるFCFの割引現在価値の総和は、876億円である。
(3) トータル
1~10年目までの割引現在価値の総和(386億円)と11年目以降の割引現在価値の総和(876億円)を合計して、この企業の事業価値(EV)は1262億円となる。 1~10年目までと11年目以降の割引現在価値の総和を合計して、この企業の事業価値(EV)は1262億円となる。